This article has been machine-translated from Chinese. The translation may contain inaccuracies or awkward phrasing. If in doubt, please refer to the original Chinese version.
I. Hash Table
1. Concept Introduction
Variable management in compilation: Dynamic search problem
- Use a search tree? -- Comparing two variable names (strings) is inefficient
- Convert strings to numbers, then process? -- This is the idea behind hash search Known search methods:
- Sequential search O(N)
- Binary search (static search) O(log2N)
- Binary search tree O(h) where h is the height of the binary search tree
- AVL tree O(log2N)
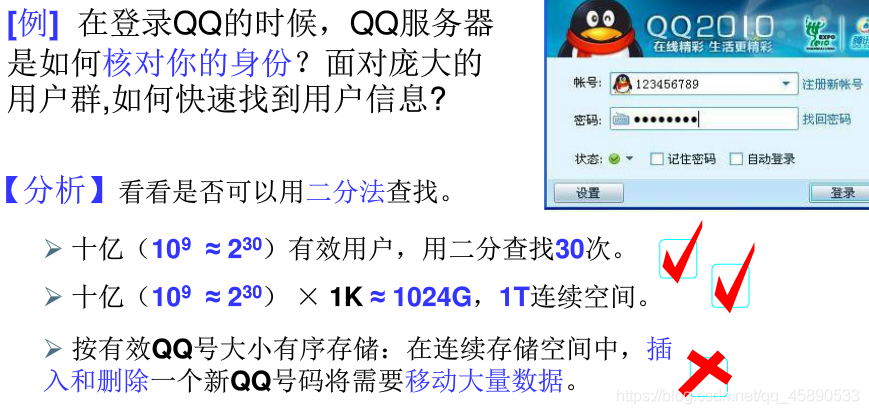
Problem: How to quickly search for the desired keyword? What if the keywords are inconvenient to compare?
The essence of searching: Finding the position of a known object
- Orderly arrangement of objects: Total order (completely ordered, e.g., binary search), partial order (some keywords have an ordering relationship, e.g., search trees)
- Directly "compute" the object's position: Hashing
Basic Operations of Hashing
- Computing position: Construct a hash function to determine the storage location of keywords
- Resolving collisions: Apply a strategy to handle cases where multiple keywords map to the same position
Time Complexity
The time complexity is nearly constant: O(1), meaning the search time is independent of the problem size!
2. Hash Search
(1) Basic Idea
- Using the keyword key as the independent variable, compute the corresponding function value h(key) through a deterministic function h (hash function), which serves as the storage address of the data object.
- Different keywords may map to the same hash address, i.e., h(keyi) = h(keyj) (when keyi != keyj), which is called a "Collision". -- A collision resolution strategy is needed.
In the absence of collisions, searching only requires computing the address using the hash function and looking it up.
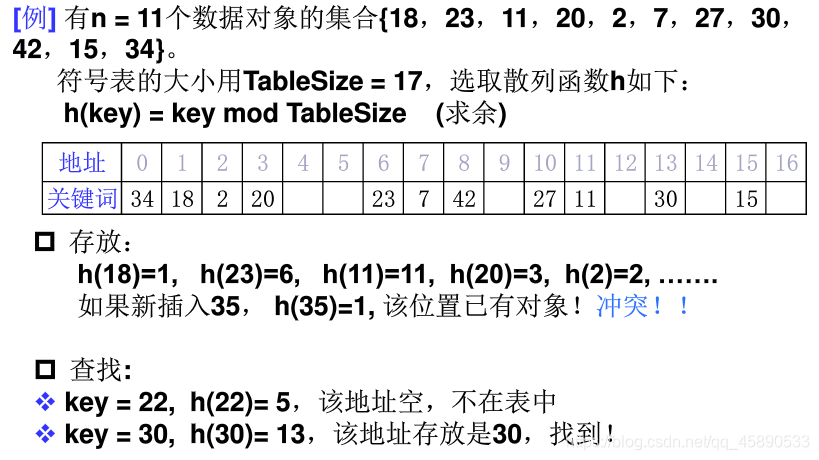
Load Factor
Load Factor: If the hash table has a space of size m and n elements are stored in it, then alpha = n / m is called the load factor of the hash table.
- As in the above figure, alpha = 11 / 17 approximately equals 0.65 If there is no overflow, then Tsearch = Tinsert = Tdelete = O(1)
Rehashing
- When the hash table has too many elements (i.e., the load factor alpha is too large), search efficiency decreases
- The practical maximum load factor is generally 0.5 <= alpha <= 0.85
- The solution is to double the hash table size. This process is called "Rehashing"
(2) Constructing Hash Functions
Two Factors
A "good" hash function should generally consider the following two factors:
- Simple computation, to improve conversion speed
- Uniform distribution of keyword addresses, to minimize collisions as much as possible.
Hash Function Construction for Numeric Keywords
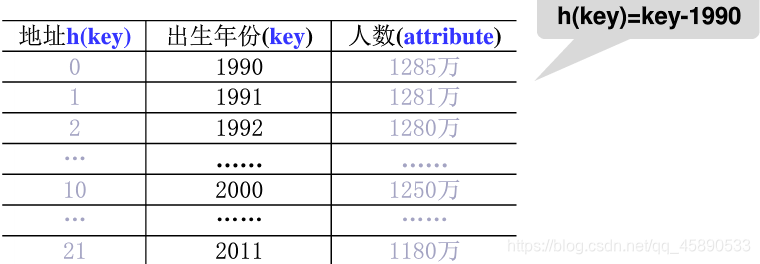
1. Direct Addressing Method
Take a linear function of the keyword as the hash address: h(key) = a * key + b (a, b are constants)
2. Division Method (Commonly Used)
Hash function: h(key) = key mod p e.g., h(key) = key % 17

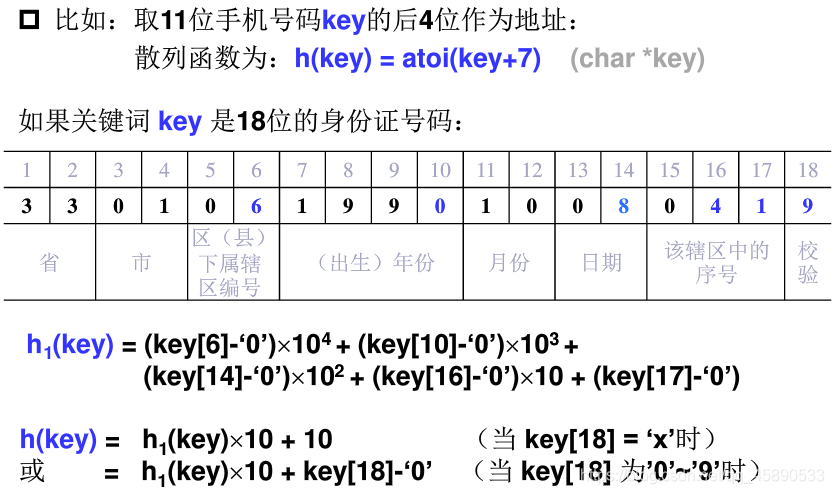
3. Digit Analysis Method
Analyze the variation of digits at each position of numeric keywords and select the more random digits as the hash address.
4. Folding Method
Split the keyword into several parts of equal digit length, then sum them up.

5. Mid-Square Method

Hash Function Construction for String Keywords
Simple Hash Function -- ASCII Code Sum Method
For a character keyword key, define the hash function as: h(key) = (sum of key[i]) mod TableSize Severe collisions!!
Simple Improvement -- First 3 Characters Shift Method
h(key) = (key[0] * 272 + key[1] * 27 + key[2]) mod TableSize Still has collisions and space waste
Good Hash Function -- Shift Method
Considers all n characters of the keyword and distributes well. h(key) = () mod TableSize Code:
typedef string DataType;//Data type
typedef int Index;//Index after hashing
//Return the index computed by the hash function
Index Hash(string Key, int TableSize) {
unsigned int h = 0; //Hash function value, initialized to 0
int len = Key.length();
for(int i = 0; i < len; ++i)
h = (h << 5) + Key[i];
return h % TableSize;
}(3) Collision Resolution in Hash Search
Common approaches for handling collisions:
- Try another position -- Open Addressing
- Organize all conflicting objects at the same position together -- Separate Chaining
Open Addressing
Open Addressing: Once a collision occurs (another element is already at that position), find another empty address according to some rule. Its advantage is that the hash table is an array with high storage efficiency and random access; its disadvantage is the "clustering" phenomenon. In open addressing, deletion must be done carefully -- only "lazy deletion" is allowed, meaning a deletion marker must be added rather than actually deleting, so that searches won't "break the chain". The space can be reused on the next insertion.
- If the i-th collision occurs, the next probed address is incremented by di. The basic formula is: hi(key) = (h(key) + di) mod TableSize (1 <= i < TableSize)
- The value of di determines different collision resolution strategies: Linear probing (di = i), Quadratic probing (di = +/- i2), Double hashing (di = i * h2(key)).
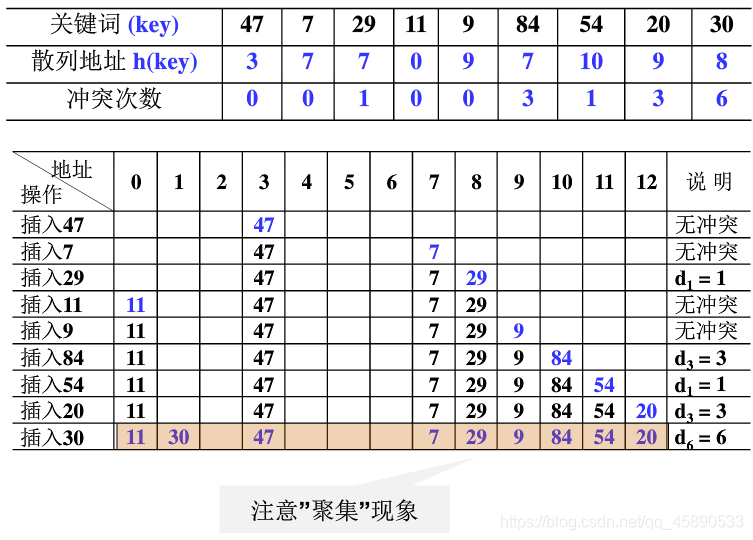
1. Linear Probing
Try the next storage addresses in the sequence 1, 2, ..., (TableSize - 1) cyclically.

2. Quadratic Probing (Secondary Probing)
Try the next storage addresses with the increment sequence 12, -12, 22, -22, ..., q2, -q2 where q <= |TableSize/2|, cyclically.

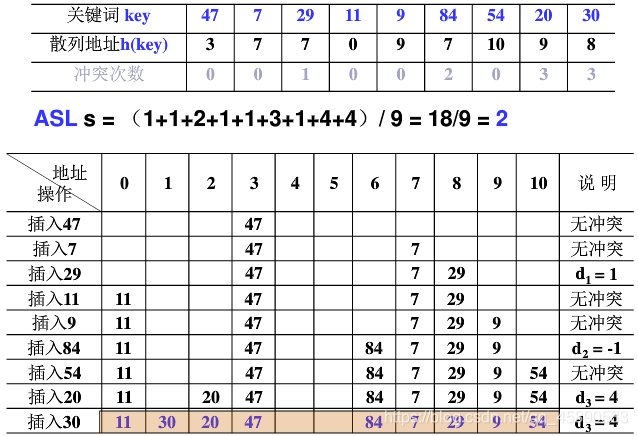
- If the hash table length TableSize is a prime number of the form 4k+3 (where k is a positive integer), then quadratic probing can probe the entire hash table space.
//Search for Key element, using quadratic probing for collision resolution
Index Find(ptrHash H, DataType Key) {
Index nowp, newp;
int Cnum = 0;//Record number of collisions
newp = nowp = Hash(Key, H->TableSize);
//Collision occurs when the position is non-empty and not the target element
while(H->Units[newp].flag != Empty && H->Units[newp].data != Key) {
++Cnum;//One more collision
if(++Cnum % 2) {
newp = nowp + (Cnum+1)*(Cnum+1)/4;//Increment is +i^2, where i is (Cnum+1)/2
if(newp >= H->TableSize)
newp = newp % H->TableSize;
} else {
newp = nowp - Cnum*Cnum/4;//Increment is -i^2, where i is Cnum/2
while(newp < 0)
newp += H->TableSize;
}
}
return newp;//Return position; if it's an empty cell, the key was not found
}3. Double Hashing
di is i * h2(key), where h2(key) is another hash function. The probe sequence becomes h2(key), 2h2(key), 3h2(key)...
- For any key, h2(key) != 0!
- The probe sequence should also ensure all hash table cells can be probed. The following form has good results: h2(key) = p - (key mod p) where p < TableSize, and both p and TableSize are prime numbers.
Separate Chaining
Separate Chaining: Store all keywords that collide at the same position in a singly linked list. Its advantage is that deletion does not require "lazy deletion," so there is no storage garbage. Its disadvantage is that the storage efficiency and search efficiency of the linked list portions are relatively low. Uneven linked list lengths can cause severe degradation in time efficiency.
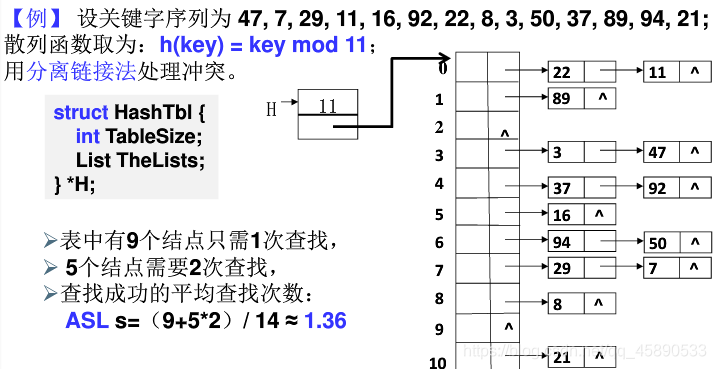
(4) Operation Set for Hash Search (Code)
Here we provide hash search for strings, using the shift method for the hash function and quadratic probing from open addressing for collision resolution. Other methods can be modified from this basis.
Definition
const int MaxSize = 100000;
typedef int Index;//Index after hashing
typedef string DataType;//Element type stored in hash cells
//Hash cell status type: has a legitimate element, empty cell, has a deleted element
typedef enum {Legitimate, Empty, Deleted} EntryType;
struct HashNode { //Hash table cell type
DataType data; //Store element
EntryType flag; //Cell status
};
struct HashTable { //Hash table type
int TableSize; //Table size
HashNode *Units; //Array storing hash cells
};
typedef HashTable *ptrHash;Getting a Prime Number
Return the smallest prime number greater than N and not exceeding MaxSize, to ensure the hash table's maximum length is prime and keyword addresses are distributed as uniformly as possible.
//Return the smallest prime number greater than N and not exceeding MaxSize
int NextPrime(int N) {
int i, p = (N%2) ? N+2 : N+1;//Start from the next odd number greater than N
while(p <= MaxSize) {
for(i = (int)sqrt(p); i >= 2; i--)
if(!(p % i)) break;//Not a prime
if(i == 2) break;//for loop ended normally, it's a prime
else p += 2;//Try the next odd number
}
return p;
}Creating an Empty Table
Create an empty table with length greater than TableSize (ensuring the length is prime).
ptrHash CreateTable(int TableSize) {
ptrHash H;
int i;
H = new HashTable;
H->TableSize = NextPrime(TableSize);
H->Units = new HashNode[H->TableSize];
for(int i = 0; i < H->TableSize; ++i)
H->Units[i].flag = Empty;
return H;
}Hash Computation
Return the index computed by the hash function. Here the keyword data type is string, using the shift method for hashing.
Index Hash(DataType Key, int TableSize) {
unsigned int h = 0; //Hash function value, initialized to 0
string str = Key.str;
int len = str.length();
for(int i = 0; i < len; ++i)
h = (h << 5) + str[i];
return h % TableSize;
}Search Operation
Search for Key element, using quadratic probing for collision resolution. Returns the position index; if the position is an empty cell, the key was not found.
Index Find(ptrHash H, DataType Key) {
Index nowp, newp;
int Cnum = 0;//Record number of collisions
newp = nowp = Hash(Key, H->TableSize);
//Collision occurs when the position is non-empty and not the target element
while(H->Units[newp].flag != Empty && H->Units[newp].data != Key) {
++Cnum;//One more collision
if(++Cnum % 2) {
newp = nowp + (Cnum+1)*(Cnum+1)/4;//Increment is +i^2, where i is (Cnum+1)/2
if(newp >= H->TableSize)
newp = newp % H->TableSize;
} else {
newp = nowp - Cnum*Cnum/4;//Increment is -i^2, where i is Cnum/2
while(newp < 0)
newp += H->TableSize;
}
}
return newp;//Return position; if it's an empty cell, the key was not found
}Insert Operation
Insert Key into the table. Returns whether insertion was successful or not; failure means the key already exists.
bool Insert(ptrHash H, DataType Key) {
Index p = Find(H, Key);
if(H->Units[p].flag != Legitimate) {//This position can accept an element
H->Units[p].flag = Legitimate;
H->Units[p].data = Key;
//Other operations
return true;
} else {//The key already exists
//Other operations
return false;
}
}(5) Performance Analysis
The search efficiency of a hash table is analyzed through the following factors:
- Average Successful Search Length (ASLs)
- Average Unsuccessful Search Length (ASLu)
Taking the example from the linear probing section, let's analyze the performance of this hash table:

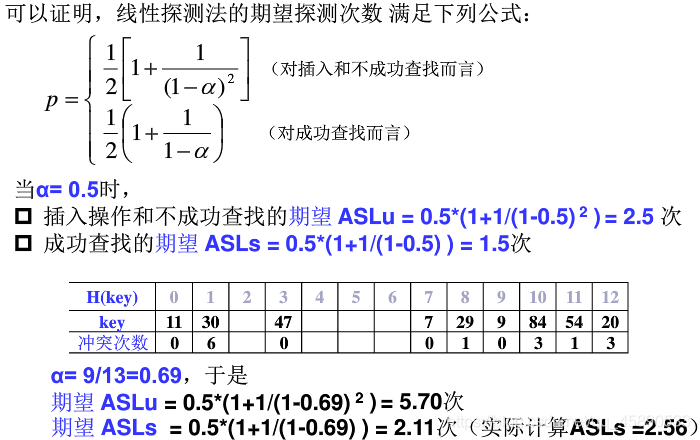
- ASLs is the average number of search comparisons for keywords in the table (i.e., the number of collisions plus 1) ASLs = (1+7+1+1+2+1+4+2+4) / 9 = 23 / 9 approximately equals 2.56
- ASLu is the average number of search comparisons for keywords not in the hash table (unsuccessful) General method: Classify keywords not in the hash table into several categories. If classified by H(key) values, here H(key) = key mod 11, we have 11 categories. ASLu is as follows: ASLu = (3+2+1+2+1+1+1+9+8+7+6) / 11 = 41 / 11 approximately equals 3.73
The number of keyword comparisons depends on how many collisions occur, which is influenced by three factors:
- Whether the hash function distributes uniformly
- The collision resolution method
- The load factor alpha of the hash table The impact of different collision resolution methods and load factors on efficiency is as follows:
1. Search Performance of Linear Probing
2. Search Performance of Quadratic Probing and Double Hashing
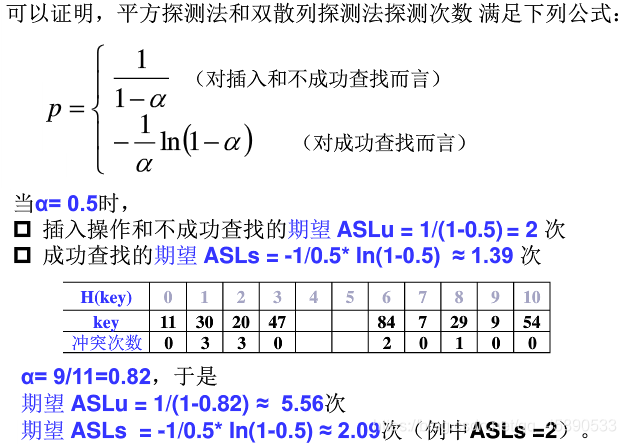
3. Search Performance of Separate Chaining

Summary
- With an appropriate h(key), the expected search efficiency of hashing is constant O(1), which is almost independent of the size n of the keyword space! It is also suitable for problems where direct keyword comparison is computationally expensive.
- This is predicated on a small alpha, so hashing is a method that trades space for time.
- The storage of hash methods is random with respect to keywords, making it inconvenient for sequential search of keywords, and also not suitable for range searches or finding maximum/minimum values.

喜欢的话,留下你的评论吧~