This article has been machine-translated from Chinese. The translation may contain inaccuracies or awkward phrasing. If in doubt, please refer to the original Chinese version.

I. Graphs

1. What is a Graph

Represents "many-to-many" relationships and contains:

• A set of vertices: usually denoted V (Vertex) for the vertex set
• A set of edges: usually denoted E (Edge) for the edge set
• An undirected edge is a vertex pair: (v, w) belongs to E, where v, w belong to V
• A directed edge <v, w> represents an edge from v to w (one-way)
• Self-loops and multiple edges are not considered

Abstract Data Type Definition

Type name: Graph Data object set: G(V, E) consists of a non-empty finite vertex set V and a finite edge set E. Operation set: For any graph G belonging to Graph, and v belonging to V, e belonging to E:

• Graph Create(): Create and return an empty graph;
• Graph InsertVertex(Graph G, Vertex v): Insert vertex v into graph G
• Graph InsertEdge(Graph G, Edge e): Insert edge e into graph G
• void DFS(Graph G, Vertex v): Depth-first traversal of graph G starting from vertex v;
• void BFS(Graph G, Vertex v): Breadth-first traversal of graph G starting from vertex v;
• void ShortestPath(Graph G, Vertex v, int Dist[]): Compute the shortest distances from vertex v to all other vertices in graph G;
• void MST(Graph G): Compute the minimum spanning tree of graph G Common terminology: Undirected graph, directed graph, network, etc.

How to Represent a Graph in a Program

Adjacency Matrix

Advantages of an adjacency matrix:

• Intuitive, simple, and easy to understand
• Convenient for checking whether an edge exists between any pair of vertices
• Convenient for finding all "adjacent vertices" (vertices directly connected by an edge) of any vertex
• Convenient for computing the "degree" of any vertex (the number of edges originating from a vertex is its "out-degree", and the number of edges pointing to a vertex is its "in-degree")
  • Undirected graph: The number of non-zero elements in the corresponding row (or column)
  • Directed graph: The number of non-zero elements in the row is the out-degree, and the number of non-zero elements in the column is the in-degree

Adjacency List

Pointer array + linked lists. Very efficient when vertices are sparse.

Advantages of an adjacency list:

• Convenient for finding all "adjacent vertices" (vertices directly connected by an edge) of any vertex
• Saves space for sparse graphs
  • Requires N head pointers + 2E nodes (each node has at least 2 fields)
• Convenient for computing the "degree" of any vertex in an undirected graph, but for directed graphs, only the out-degree can be computed.

2. Graph Traversal

DFS (Depth-First Search)

Depth-First Search (DFS) explores each possible branch path as deep as possible, and each node can only be visited once. Pseudocode:

void DFS(Vertex V) {
 visited[V] = true;
 for(each adjacent vertex W of V)
  if (!visited[W])
   DFS(W);
}

BFS (Breadth-First Search)

Breadth-First Search (BFS) is implemented using a queue (FIFO). Pseudocode:

void BFS(Vertex V) {
 visited[V] = true;
 Enqueue(V, Q);//Enqueue the vertex
 while(!IsEmpty(Q)) {//Search ends when the queue is empty
  V = Dequeue(Q);//V is the front element of the queue
  for(each adjacent vertex W of V) {
   if ( !visited[W] ) {
    visited[W] = true;//Mark the vertex as visited
    Enqueue(W, Q);//Enqueue the vertex
   }
  }
 }
}

What if the Graph is Disconnected?

• Path: The path from V to W is a set of vertices {V, V1, V2, ..., Vn, W} where any pair of adjacent vertices has an edge in the graph. The path length is the number of edges in the path (if weighted, it is the sum of all edge weights). If all vertices from V to W are distinct, it is called a simple path.
• Connected: If there exists an (undirected) path from V to W, then V and W are connected.
• Cycle: A path where the starting point equals the ending point.
• Connected Graph: Any two vertices in the graph are connected.
• Connected Component: A maximal connected subgraph of an undirected graph.
  • Maximum vertices: Adding one more vertex would make it disconnected
  • Maximum edges: Includes all edges connecting the vertices within the subgraph

    

• Strongly Connected: In a directed graph, if there exist bidirectional paths between vertices V and W, then V and W are strongly connected.
• Strongly Connected Graph: Any two vertices in a directed graph are strongly connected.
• Strongly Connected Component: A maximal strongly connected subgraph of a directed graph.

  

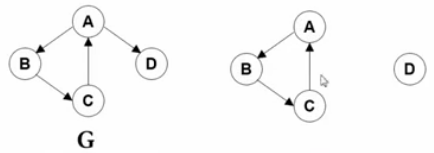
Each call to DFS actually traverses the entire connected component containing V. The same applies to BFS.

void ListComponents ( Graph G ) {//Traverse connected components
 for (each V in G)
  if ( !visited[V] ) {
   DFS( V );
  }
}

3. How to Build a Graph

(1) Building a Graph Represented by an Adjacency Matrix

Definition

const int MaxVertexNum = 100;
typedef int DataType;
typedef bool WeightType;
typedef struct GNode *PtrToGNode;
struct GNode {
    int Nv;//Number of vertices
    int Ne;//Number of edges
    WeightType G[MaxVertexNum][MaxVertexNum];
    DataType Data[MaxVertexNum];//Store vertex data
};
typedef PtrToGNode MGraph;//Graph type stored as adjacency matrix

Initialization

Initialize a graph with VertexNum vertices but no edges.

typedef int Vertex;
MGraph CreateGraph(int VertexNum) {
    Vertex V, W;
    MGraph Graph;
    Graph = (MGraph) malloc(sizeof(struct GNode));
    Graph->Nv = VertexNum;
    Graph->Ne = 0;
    //Vertex numbering starts from 0 to Graph->Nv-1
    for (V = 0; V < Graph->Nv; V++) {
        for(W = 0; W < Graph->Nv; W++) {
            Graph->G[V][W] = 0; //For directed graphs, 0 can be changed to INF, etc.
        }
    }
    return Graph;
}

Inserting Edges into the Graph

Edge definition

typedef struct ENode *PtrToENode;
struct ENode {
    Vertex V1, V2;//Directed edge <V1,V2>
    WeightType Weight;//Weight
};
typedef PtrToENode Edge;

Insert operation

void InsertEdge(MGraph Graph, Edge E) {
    //Insert edge <V1,V2>
    Graph->G[E->V1][E->V2] = E->Weight;
    //For undirected graphs, also insert edge <V2,V1>
    Graph->G[E->V2][E->V1] = E->Weight;
}

Complete Construction of an MGraph

Input format

Nv Ne V1 V2 Weight ...

MGraph BuildGraph() {
    MGraph Graph;
    Edge E;
    Vertex V;
    int Nv;
    cin >> Nv;
    Graph = CreateGraph(Nv);//Create a graph with Nv vertices
    cin >> Graph->Ne;//Number of edges Ne
    if(Graph->Ne != 0) {
        E = (Edge)malloc(sizeof(struct ENode));
        for (int i = 0; i < Graph->Ne; i++) {
            cin >> E->V1 >> E->V2 >> E->Weight;
            InsertEdge(Graph, E);
        }
    }
    //If vertices have data, read the data
    for(V = 0; V < Graph->Nv; V++) {
        cin >> Graph->Data[V];
    }
    return Graph;
}

(2) Building a Graph Represented by an Adjacency List

Can be modified based on the adjacency matrix approach.

Definition

const int MaxVertexNum = 100;
typedef int DataType;
typedef int Vertex;
typedef bool WeightType;
//Adjacency list definition
typedef struct AdjVNode *PtrToAdjVNode;
struct AdjVNode {
    Vertex AdjV;//Adjacent vertex index
    WeightType Weight;//Edge weight
    PtrToAdjVNode Next;
};

typedef struct VNode {
    PtrToAdjVNode FirstEdge;
    DataType Data;//Store vertex data
}AdjList;

typedef struct GNode *PtrToGNode;
struct GNode {
    int Nv;//Number of vertices
    int Ne;//Number of edges
    AdjList G;//Adjacency list
};
typedef PtrToGNode LGraph;//Graph type stored as adjacency list

LGraph Initialization

LGraph CreateGraph(int VertexNum) {
    Vertex V, W;
    LGraph Graph;
    Graph = (LGraph) malloc(sizeof(struct GNode));
    Graph->Nv = VertexNum;
    Graph->Ne = 0;
    //Vertex numbering starts from 0 to Graph->Nv-1
    for (V = 0; V < Graph->Nv; V++) {
        Graph->G[V].FirstEdge = NULL;
    return Graph;
}

Inserting Edges into an LGraph

typedef struct ENode *PtrToENode;
struct ENode {
    Vertex V1, V2;//Directed edge <V1,V2>
    WeightType Weight;//Weight
};
typedef PtrToENode Edge;
void InsertEdge(LGraph Graph, Edge E){
    PtrToAdjVNode NewNode;
    //Insert edge <V1,V2>
    //Create a new adjacent node for V2
    NewNode = (PtrToAdjVNode) malloc(sizeof(struct AdjVNode));
    NewNode->AdjV = E->V2;
    NewNode->Weight = E->Weight;
    //Insert V2 adjacent node at the head of V1's list
    NewNode->Next = Graph->G[E->V1].FirstEdge;
    Graph->G[E->V1].FirstEdge = NewNode;

    //For undirected graphs, also insert edge <V2,V1>
    //Create a new adjacent node for V1
    NewNode = (PtrToAdjVNode) malloc(sizeof(struct AdjVNode));
    NewNode->AdjV = E->V1;
    NewNode->Weight = E->Weight;
    //Insert V1 adjacent node at the head of V2's list
    NewNode->Next = Graph->G[E->V2].FirstEdge;
    Graph->G[E->V1].FirstEdge = NewNode;
}

Complete Construction of an LGraph

Only need to replace MGraph with LGraph and make minor modifications when storing Data.

LGraph BuildGraph() {
    LGraph Graph;
    Edge E;
    Vertex V;
    int Nv;
    cin >> Nv;
    Graph = CreateGraph(Nv);//Create a graph with Nv vertices
    cin >> Graph->Ne;//Number of edges Ne
    if(Graph->Ne != 0) {
        E = (Edge)malloc(sizeof(struct ENode));
        for (int i = 0; i < Graph->Ne; i++) {
            cin >> E->V1 >> E->V2 >> E->Weight;
            InsertEdge(Graph, E);
        }
    }
    //If vertices have data, read the data
    for(V = 0; V < Graph->Nv; V++) {
        cin >> Graph->G[V].Data;
    }
    return Graph;
}

II. Shortest Path Problem

1. Concept Introduction

• In a network, find the path with the minimum sum of edge weights among all paths between two different vertices
  • This path is the Shortest Path between the two vertices
  • The first vertex is called the Source
  • The last vertex is called the Destination

2. Problem Classification

• Single-source shortest path problem: Starting from a fixed source, find the shortest paths to all other vertices
  • (Directed) unweighted graph
  • (Directed) weighted graph
• Multi-source shortest path problem: Find the shortest paths between any two vertices

2. Single-Source Shortest Path Algorithm for Unweighted Graphs

Find the shortest paths to each vertex in increasing order, very similar to the BFS approach!

First, define an array dist, where dist[W] stores the shortest distance from S to W, S is the starting point, dist[S] = 0. dist needs to be initialized to -1 (or infinity) to facilitate later checks of whether a vertex has been visited. Then define an array path, where path[W] stores a vertex on the path from S to W. Both the dist and path arrays should first be initialized to -1, then set dist[S] to 0, enqueue the starting point and begin visiting. Pseudocode:

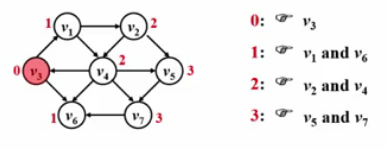
void Unweighted(Vertex S) {
 Enqueue(S, Q);
 while(!IsEmpty(Q)) {
  V = Dequeue(Q);
  for (each adjacent vertex W of V)
   if(dist[W] == -1) {
    dist[W] = dist[V]+1;
    path[W] = V;
    Enqueue(W, Q);
   }
 }
}

3. Single-Source Shortest Path Algorithm for Weighted Graphs

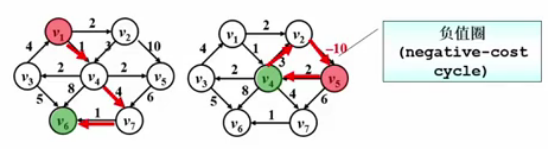
Dijkstra's Algorithm

• Let S = {source s + vertices v_i whose shortest paths have been determined}
• For any unvisited vertex v, define dist[v] as the shortest path length from s to v, but this path only passes through vertices in S, i.e., the minimum length of path {s -> (v_i belonging to S) -> v}
• If paths are generated in increasing order, then:
  • The true shortest path must only pass through vertices in S (provable by contradiction)
  • Each time, select the unvisited vertex with the smallest dist for inclusion (greedy approach)
  • Adding a vertex v to S may affect the dist value of another vertex w! (So we must check all adjacent vertices w of v!)
  • dist[w] = min{ dist[w], dist[v] + weight of <v,w> } dist initialization: All adjacent vertices W of S can be initialized with the weight between s and w; others are defined as positive infinity.

Pseudocode:

void Dijkstra(Vertex s) {
 while (1){
  V = the unvisited vertex with the smallest dist;
  if (no such V exists)
   break;
  collected[V] = true;
  for (each adjacent vertex W of V)
   if(collected[W] == false)
    if(dist[V] + E<v,w> < dist[W]) {
     dist[W] = dist[V]+E<v,w>;
     path[W] = V;
    }
 }
}//Cannot handle negative edges

In the pseudocode, dist[W] = dist[V] + E_<V,W> is not simply an assignment but means that if a shorter distance is found, it should be updated to the shorter distance.

Dijkstra Core Code

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
using namespace std;
const int maxn = 1005;
const int inf  = 0x3f3f3f;
int T,N,x,y,z;
int edge[maxn][maxn];
int dist[maxn];
bool vis[maxn];
void init() {
    for(int i = 1; i <= N; ++i) {
        for(int j = 1; j <= N; ++j) {
            edge[i][j] = inf;
        }
        edge[i][i] = 0;
    }
}
void Dijstra(int u) {
    for(int i = 1; i <= N; ++i) {
        vis[i] = false;
        dist[i] = edge[u][i];
    }
    vis[u] = true;
    for(int i = 1; i <= N; ++i) {
        int t, mindis = inf;
        for(int j = 1; j <= N; ++j) {
            if(!vis[j] && dist[j] < mindis) {
                mindis = dist[j];
                t = j;
            }
        }
        vis[t] = true;
        for(int j = 1; j <= N; ++j)
            if(!vis[j] && dist[j] > edge[t][j] + dist[t])
                dist[j] = edge[t][j] + dist[t];
    }
}

III. Minimum Spanning Tree

1. What is a Minimum Spanning Tree (MST)

• It is a tree
  • No cycles
  • |V| vertices must have exactly |V|-1 edges
• It is a spanning tree
  • Contains all vertices
  • All |V|-1 edges are from the graph

    

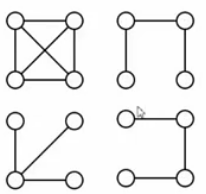
  • Adding any edge to the spanning tree will certainly create a cycle
• The sum of edge weights is minimum

A minimum spanning tree is equivalent to graph connectivity.

2. Solving the Minimum Spanning Tree Problem

Greedy algorithms are usually involved:

• "Greedy": Take the best at each step
• "Best": The edge with the smallest weight
• Constraints:
  • Can only use edges that exist in the graph
  • Must use exactly |V|-1 edges
  • No cycles allowed

This has been covered in another blog post. Graph Theory -- Solving the Minimum Spanning Tree Problem (Kruskal's Algorithm & Prim's Algorithm)