Data Structure Study Notes <4> Binary Trees | Notes / 数据结构

This article has been machine-translated from Chinese. The translation may contain inaccuracies or awkward phrasing. If in doubt, please refer to the original Chinese version.

I. What is a Tree

1. Definition of a Tree

Tree: A finite collection of n (n >= 0) nodes. When n = 0, it is called an empty tree; For any non-empty tree (n > 0), it has the following properties:

There is a special node called the "Root" in the tree, denoted by r.
The remaining nodes can be divided into m (m > 0) mutually disjoint finite sets T1, T2, ..., Tm, where each set is itself a tree, called a "SubTree" of the original tree.
Subtrees are disjoint.
Except for the root node, each node has exactly one parent node.
A tree with N nodes has N-1 edges.

2. Some Basic Terminology of Trees

1. Degree of a Node: The number of child nodes a node has 2. Degree of a Tree: The maximum degree among all nodes is called the degree of the tree 3. Leaf Node: A node with degree 0 4. Parent Node: If a node has a preceding node, that preceding node is its parent node. If there is no preceding node, then this node has no parent. 5. Child Node: If node A is the parent of node B, then B is called a child node of A; child nodes are also called children 6. Sibling Node: Nodes that share the same parent node are sibling nodes. 7. Path and Path Length: The path from node n1 to nk is a node sequence n1, n2, ..., nk, where ni is the parent of ni+1. The number of edges contained in the path is the path length. 8. Ancestor Node: All nodes along the path from the root to a certain node are ancestors of that node. 9. Descendant Node: All nodes in the subtree of a certain node are its descendants. 10. Level of a Node: The root node is defined as level 1, and the level of any other node is its parent's level plus 1. 11. Depth of a Tree: The maximum level of all nodes in the tree is the depth of the tree. 12. Forest: A collection of m disjoint trees.

II. Representation of Trees

1. Child-Sibling Representation

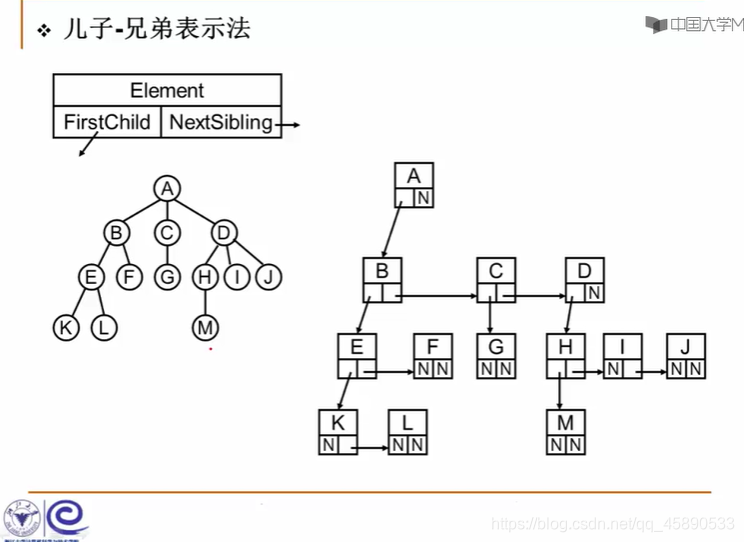
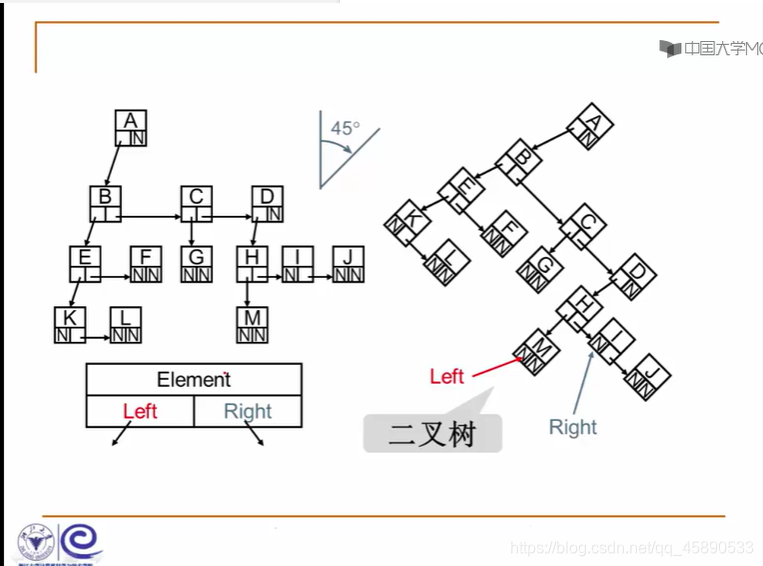
III. Binary Trees

1. Definition

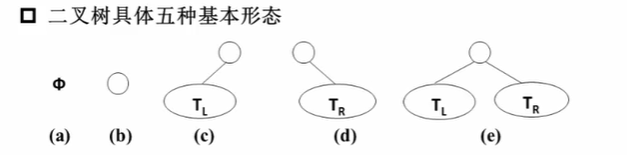
Binary Tree T: A finite set of nodes. This set can be empty. If not empty, it consists of a root node and two disjoint binary trees called its left subtree TL and right subtree TR. A binary tree has five basic forms: a) empty tree b) only one node c) one node and a left subtree d) one node and a right subtree e) one node with both left and right subtrees

PS: The subtrees of a binary tree have a left-right order distinction

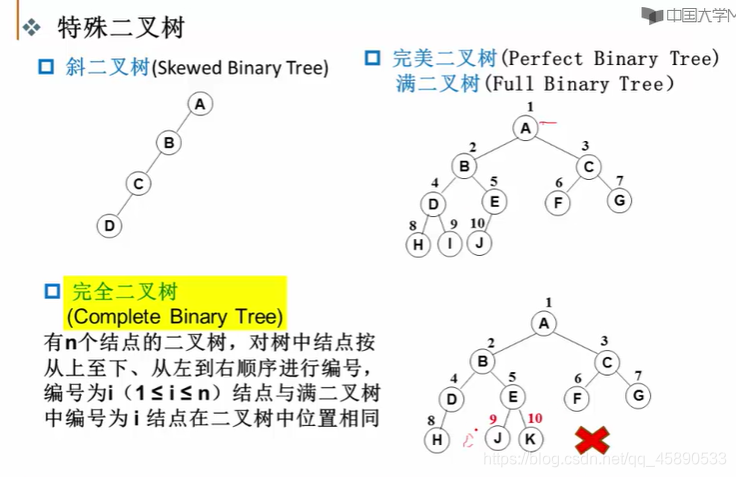
Several special binary trees

Abstract Data Type Definition of Binary Tree Type name: Binary Tree Data object set: A finite set of nodes. If not empty, it consists of a root node and its left and right binary subtrees. Operation set: BT belongs to BinTree, Item belongs to ElementType, important operations include:

Boolean IsEmpty(BinTree BT); //Determine if BT is empty
void Traversal(BinTree BT); //Traversal, visit each node in a certain order;
BinTree CreatBinTree(); //Create a binary tree

Common traversal methods:

void PreOrderTraversal(BinTree BT); //Pre-order --- root, left subtree, right subtree
void InOrderTraversal(BinTree BT); //In-order --- left subtree, root, right subtree
void PostOrderTraversal(BinTree BT); //Post-order --- left subtree, right subtree, root
void LevelOrderTraversal(BinTree BT); //Level-order traversal, top to bottom, left to right

2. Important Properties of Binary Trees

The maximum number of nodes at level i of a binary tree is 2^i-1, i >= 1.
A binary tree of depth k has a maximum total number of nodes of 2^k-1, k >= 1.
For any non-empty binary tree T, if n0 represents the number of leaf nodes and n2 is the number of non-leaf nodes with degree 2, then they satisfy the relation n0 = n2 + 1.
A complete binary tree with n nodes must have a depth k of log₂n+1

3. Storage Structures of Binary Trees

1. Sequential Storage

Complete Binary Tree: Store n nodes of a complete binary tree in top-to-bottom, left-to-right order. The parent-child relationship of nodes:

For a non-root node (index i > 1), the index of its parent node is [i / 2]; (floor division)
The index of the left child of a node (index i) is 2i (2i <= n, otherwise it has no left child)
The index of the right child of a node (index i) is 2i+1 (2i + 1 <= n, otherwise it has no right child)

General binary trees can also use this sequential storage structure, but it may waste space

Full Binary Tree: A binary tree where every level, except possibly the last, has all nodes with two children, distinguished from a complete binary tree

2. Linked Storage

(1) Definition

typedef struct TreeNode *BinTree;
typedef BinTree Position;
struct TreeNode {
  ElementType Data;
  BinTree Left;
  BinTree Right;
}

(2) Traversal (Recursive Implementation)

Pre-order Traversal

Visit the root node first; 2. Pre-order traverse the left subtree; 3. Pre-order traverse the right subtree.

void PreOrderTraversal(BinTree BT) {
 if(BT) {
  printf("%d", BT->Data);
  PreOrderTraversal( BT->Left);
  PreOrderTraversal( BT->Right);
 }
}

In-order Traversal

In-order traverse the left subtree; 2. Visit the root node; 3. In-order traverse the right subtree.

void InOrderTraversal(BinTree BT) {
 if(BT) {
  InOrderTraversal( BT->Left);
  printf("%d", BT->Data);
  InOrderTraversal( BT->Right);
 }
}

Post-order Traversal

Post-order traverse the left subtree; 2. Post-order traverse the right subtree; 3. Visit the root node.

void PostOrderTraversal(BinTree BT) {
 if(BT) {
  PostOrderTraversal( BT->Left);
  PostOrderTraversal( BT->Right);
  printf("%d", BT->Data);
 }
}

(2) Traversal (Non-recursive Implementation)

Basic idea: Use a stack or queue

Non-recursive In-order Traversal Algorithm

When encountering a node, push it onto the stack and traverse its left subtree;
When the left subtree traversal is complete, pop the node from the stack top and visit it;
Then follow its right pointer to in-order traverse the right subtree of that node.

void InOrderTraversal(BinTree BT) {
 BinTree T = BT;
 Stack S = CreatStack(MaxSize);//Create and initialize stack S
 while( T || !IsEmpty(S) ) {
  while(T) {//Keep going left and push nodes along the way onto the stack
   Push(S, T);
   T = T->Left;
  }
  if( !IsEmpty(S) ) {
   T = Pop(S); //Pop node from stack
   printf("%5d", T->Data);//Visit node
   T = T->Right;//Turn to right subtree
  }
 }
}

Level-order Traversal

Requires a storage structure to hold nodes that are not visited immediately (stack or queue) Queue implementation: Traversal starts from the root node, first enqueue the root node, then execute the loop: dequeue a node, visit that node, enqueue its left and right children. 1. Enqueue the root node; 2. Dequeue an element from the queue; 3. Visit the node pointed to by that element; 4. If the left and right child nodes of that element's node are non-null, enqueue their left and right child pointers in order.

void LevelOrderTraversal(BinTree BT) {
 Queue Q;  BinTreee T;
 if ( !BT ) return; //Return directly if empty tree
 Q = CreateQueue(MaxSize);//Create and initialize queue Q
 AddQ(Q, BT);
 while( !IsEmpty(Q) ) {
  T = DeleteQ(Q);
  printf("%d\n", T->Data);//Visit node
  if(T->Left) AddQ(Q, T->Left);//Enqueue left child
  if(T->Right) AddQ(Q, T->Right);//Enqueue right child
 }
}

Supplementary Knowledge > Search as a Basic Data Management Operation: Given a key K, find a record with the same key from a collection R. It can be divided into static search and dynamic search. Static Search: Records in the collection are fixed, with no insertion or deletion operations, only search. Method 1: Sequential search (sentinel concept: set a value at the boundary of the array; when the sentinel is hit, the loop can end, saving one branch check) Complexity O(n); Method 2: Binary search (prerequisite: the array must be contiguous and sorted) Dynamic Search: Records in the collection change dynamically; besides search, insertion and deletion may also occur.