This article has been machine-translated from Chinese. The translation may contain inaccuracies or awkward phrasing. If in doubt, please refer to the original Chinese version.
In the previous post, we mentioned that the RMQ problem can be handled using the Sparse Table algorithm, but when online modifications are needed, the segment tree is a better choice. As shown in the figure, a segment tree is clearly a binary search tree.
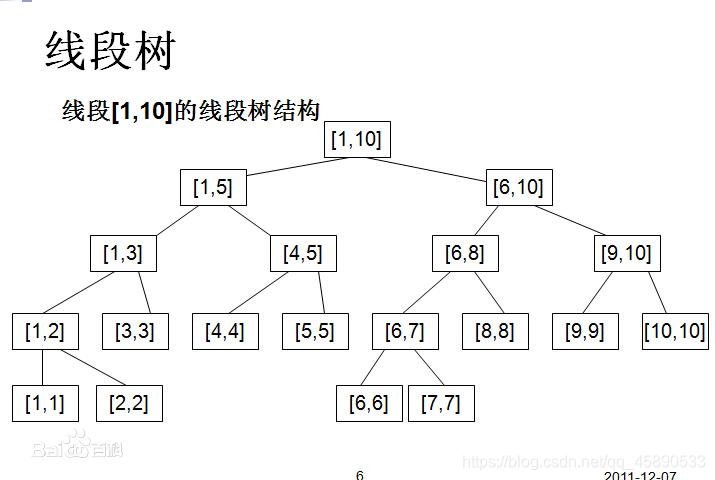
- The segment tree is stored in an array. The array size is generally allocated as 4*n times the original array (more precisely, round n up to the next power of 2 and then multiply by 2, e.g., 5 -> 8 -> 16).
- In the segment tree array, if a node’s index is n, then its left child index is 2*n (written as n << 1), and its right child index is 2*n+1 (written as n << 1 | 1).
- The root node is defined as 1.
I. Querying Range Extremes (Point Update)
Template problem: hihoCoder #1077 RMQ Problem Revisited - Segment Tree
Problem summary: Given an array A, each operation is either a query or an update. Here, queries ask for the minimum value in the range l to r, or updates change the value at index p to v.
The segment tree maintains extreme values. To change it to query for the maximum, simply replace all min with max and change inf to 0.
1. Building the Tree
void pushup(int rt) {//Update node info - using minimum as example, can be changed to maximum
Tree[rt] = min(Tree[rt << 1], Tree[rt << 1|1]);
}
void Build(int l, int r, int rt) {//[l,r] represents the interval, rt is the actual storage index
if (l == r) {//Reached a leaf node
Tree[rt] = A[l];
return;
}
int mid = l+r>>1;
Build(l,mid,rt << 1);//Build the left subtree first
Build(mid+1,r,rt << 1 | 1);//Then build the right subtree
pushup(rt);//Update info using left and right children
}2. Update
When called, parameters are: root node index, modification position p, new value v, and the affected interval (i.e., 1 to n).
void Update_point(int rt, int p, int val, int l, int r) { //Point update
if (l == r) {
Tree[rt] = val;
return;
}
int mid = (l+r) >> 1;
if (p <= mid)//If the position to modify is in the left half, update left subtree
Update_point(rt<<1, p, val, l, mid);
else Update_point(rt<<1|1, p, val, mid+1, r);//Otherwise update right subtree
pushup(rt);//Update current node
}3. Query
This is the key part. When called, parameters are: root node, full interval (1 to n), and query interval (x to y). Note: The query interval is passed down unchanged. When the sub-interval l to r is contained within the query interval, we can return.
int query(int rt, int l, int r,int x, int y) {//Query min/max/sum from node rt in range L to R - using minimum as example
if (x <= l && r <= y) {//When l~r is a sub-interval of the query interval, return current node value directly
return Tree[rt];
}
int mid = l+r >> 1;
int ans = inf;//For maximum, change this to 0
if (x <= mid) //If the left endpoint of the current interval <= mid, we must query the left half
ans = min(query(rt<<1,l,mid,x,y), ans);
if (y > mid)//If the right endpoint of the current interval > mid, we must query the right half
ans = min(query(rt<<1|1,mid+1,r,x,y), ans);
return ans;
}Complete Code
#include <iostream>
#include <algorithm>
using namespace std;
//Definitions
const int maxn = 1000005;
const int inf = 0x3f3f3f;
int Tree[maxn<<2];
int A[maxn];
int n;
void pushup(int rt) {//Push up to update node info - using minimum as example, can be changed to maximum
Tree[rt] = min(Tree[rt << 1], Tree[rt << 1|1]);
}
void Build(int l, int r, int rt) {//[l,r] represents the interval, rt is the actual storage index
if (l == r) {//Reached a leaf node
Tree[rt] = A[l];
return;
}
int mid = l+r>>1;
Build(l,mid,rt << 1);//Build the left subtree first
Build(mid+1,r,rt << 1 | 1);//Then build the right subtree
pushup(rt);//Update info using left and right children
}
void Update_point(int rt, int p, int val, int l, int r) { //Point update
if (l == r) {
Tree[rt] = val;
return;
}
int mid = (l+r) >> 1;
if (p <= mid)//If the position to modify is in the left half, update left subtree
Update_point(rt<<1, p, val, l, mid);
else Update_point(rt<<1|1, p, val, mid+1, r);//Otherwise update right subtree
pushup(rt);//Update current node
}
int query(int rt, int l, int r,int x, int y) {//Query min/max/sum from node rt in range L to R - using minimum as example
if (x <= l && r <= y) {//When l~r is a sub-interval of the query interval, return current node value directly
return Tree[rt];
}
int mid = l+r >> 1;
int ans = inf;//For maximum, change this to 0
if (x <= mid) //If the left endpoint of the current interval <= mid, we must query the left half
ans = min(query(rt<<1,l,mid,x,y), ans);
if (y > mid)//If the right endpoint of the current interval > mid, we must query the right half
ans = min(query(rt<<1|1,mid+1,r,x,y), ans);
return ans;
}
int main(){
ios::sync_with_stdio(false);
cin >> n;
for(int i = 1; i <= n; i++) {
cin >> A[i];
}
Build(1,n,1);
int T;
cin >> T;
while(T--) {
int a, b, c;
cin >> a >> b >> c;
if (a == 1) {
Update_point(1,b,c,1,n);
} else {
int ans = query(1,1,n,b,c);
cout << ans << endl;
}
}
return 0;
}II. Range Update (Sum, Difference, Product, Quotient, etc.)
1. Range Addition Operation
Luogu P3372 [Template] Segment Tree 1
Summary: Given a sequence, you need to perform two types of operations: 1. Add k to every element in a range. 2. Query the sum of elements in a range.
Detailed solution
The pros already wrote such detailed explanations, why am I even writing this
Well, typing it out once for my own reference isn’t bad
We can use a segment tree to maintain range sums. For modifications, we perform range updates, which require a lazy tag array. Point update is essentially a special case of range update.
Pushdown Operation
Push down: since the lazy tag add records the effect on child nodes, we need a function to propagate the effect downward.
inline void f(int rt, int l, int r, ll k) {//Apply the effect of k to the current node and update its lazy tag
Tree[rt] += k * (r-l+1);//Range sum - we're maintaining range sums, so each element in the range gets k added
add[rt] += k;
}
void pushdown(int rt, int l, int r) {
int mid = l+r >>1;
f(rt<<1, l, mid, add[rt]);//Update left child's lazy tag and its maintained value (range sum)
f(rt<<1|1, mid+1, r, add[rt]);//Update right child's lazy tag and its maintained value (range sum)
add[rt] = 0;//Reset current lazy tag to 0
}Range Update
void Update_section(int rt, int val, int l, int r, int rl, int rr) { //Range update
if (rl <= l && r <= rr) {//When the current interval is a sub-interval of the update range, directly update value and lazy tag
f(rt, l, r, val);
return;
}
pushdown(rt, l, r);//Before the next recursion, push down the current node's effect, then update
int mid = (l+r) >> 1;
if (rl <= mid)//If the update range affects the left half, update left subtree
Update_section(rt<<1, val, l, mid, rl, rr);
if (rr > mid)
Update_section(rt<<1|1, val, mid+1, r, rl, rr);//Otherwise update right subtree
pushup(rt);//Push up
}Complete Code
#include <iostream>
#include <algorithm>
using namespace std;
//Definitions
typedef long long ll;
const int maxn = 1000005;
const int inf = 0x3f3f3f;
ll add[maxn<<2];//Lazy tag - the effect on all child nodes, not including itself
ll Tree[maxn<<2];
ll A[maxn];
int n, T;
inline void pushup(int rt) {//Push up to update node info - use left and right children to update current node
Tree[rt] = Tree[rt << 1]+Tree[rt << 1|1];
}
inline void f(int rt, int l, int r, ll k) {//Apply the effect of k to the current node and update its lazy tag
Tree[rt] += k * (r-l+1);//Range sum - we're maintaining range sums, so each element in the range gets k added
add[rt] += k;
}
void pushdown(int rt, int l, int r) {
int mid = l+r >>1;
f(rt<<1, l, mid, add[rt]);//Update left child's lazy tag and its maintained value (range sum)
f(rt<<1|1, mid+1, r, add[rt]);//Update right child's lazy tag and its maintained value (range sum)
add[rt] = 0;//Reset current lazy tag to 0
}
void Build(int l, int r, int rt) {//[l,r] represents the interval, rt is the actual storage index
add[rt] = 0;
if (l == r) {//Reached a leaf node
Tree[rt] = A[l];
return;
}
int mid = l+r>>1;
Build(l,mid,rt << 1);//Build the left subtree first
Build(mid+1,r,rt << 1 | 1);//Then build the right subtree
pushup(rt);//Update info using left and right children
}
void Update_section(int rt, int val, int l, int r, int rl, int rr) { //Range update
if (rl <= l && r <= rr) {//When the current interval is a sub-interval of the update range, directly update value and lazy tag
f(rt, l, r, val);
return;
}
pushdown(rt, l, r);//Before the next recursion, push down the current node's effect, then update
int mid = (l+r) >> 1;
if (rl <= mid)//If the update range affects the left half, update left subtree
Update_section(rt<<1, val, l, mid, rl, rr);
if (rr > mid)
Update_section(rt<<1|1, val, mid+1, r, rl, rr);//Otherwise update right subtree
pushup(rt);//Push up
}
ll query(int rt, int l, int r,int x, int y) {//Query range sum of x~y from node rt in l to r - using minimum as example
if (x <= l && r <= y) {//When l~r is a sub-interval of the query interval, return current node value directly
return Tree[rt];
}
int mid = l+r >> 1;
ll ans = 0;
pushdown(rt, l, r);
if (x <= mid) //If the left endpoint of the current interval <= mid, we must query the left half
ans += query(rt<<1,l,mid,x,y);
if (y > mid)//If the right endpoint of the current interval > mid, we must query the right half
ans += query(rt<<1|1,mid+1,r,x,y);
return ans;
}
int main(){
ios::sync_with_stdio(false);
cin >> n >> T;
for(int i = 1; i <= n; i++) {
cin >> A[i];
}
Build(1,n,1);
while(T--) {
int a, l, r;
cin >> a;
if (a == 1) {
int k;
cin >> l >> r >> k;
Update_section(1, k, 1, n, l, r);
} else {
cin >> l >> r;
ll ans = query(1, 1, n, l, r);
cout << ans << endl;
}
}
return 0;
}2. Range Addition and Multiplication Operations (More Complete)
Luogu P3373 [Template] Segment Tree 2
Detailed solution
This problem extends the previous one by allowing both multiplication and addition on a range. This requires two lazy tag arrays: add and mul. When updating lazy tags, note that updating add only updates add, but updating mul must also update add (multiply add by k).
Multiply first, then add!!
Multiply first, then add!!!
Multiply first, then add!!!
Important enough to say three times.
Changes to the Pushdown Operation
The main change is in the f function. Note that the f function’s purpose is to apply all effects (from lazy tags) of the parent node ft to the current node rt, and update rt’s lazy tags.
inline void f(int rt, int l, int r, int ft) {//Apply all effects of parent node ft to current node rt, update its lazy tags
//Multiply first, then add!! Update value
Tree[rt] = (Tree[rt] * mul[ft]) % p;
Tree[rt] = (Tree[rt] + add[ft] * (r-l+1)) % p;
//Update lazy tags: mul is directly updated (*parent's mul)
mul[rt] = (mul[rt] * mul[ft]) % p;
//add should first *parent's mul tag, then +parent's add tag!!!
add[rt] = (add[rt] * mul[ft]) % p;
add[rt] = (add[rt] + add[ft]) % p;
}
void pushdown(int rt, int l, int r) {
int mid = l+r >>1;
f(rt<<1, l, mid, rt);//Update left child's lazy tags and maintained value
f(rt<<1|1, mid+1, r, rt);//Update right child's lazy tags and maintained value
add[rt] = 0;
mul[rt] = 1;//Reset current lazy tags
}Changes to the Update Operation (Two Types)
Addition update:
void Update_section_add(int rt,int val, int l, int r, int rl, int rr) { //Range update +val
if (rl <= l && r <= rr) {//When current interval is a sub-interval of update range, directly update value and lazy tag
Tree[rt] = (Tree[rt] + val * (r-l+1)) % p;//Apply +val effect to current node and update its lazy tag
add[rt] = (add[rt] + val) % p;
return;
}
pushdown(rt, l, r);//Before next recursion, push down the effect
int mid = (l+r) >> 1;
if (rl <= mid)//If update range affects left half, update left subtree
Update_section_add(rt<<1, val, l, mid, rl, rr);
if (rr > mid)
Update_section_add(rt<<1|1, val, mid+1, r, rl, rr);//Otherwise update right subtree
pushup(rt);//Backtrack - push up
}Multiplication update - multiplication affects the addition lazy tag!
void Update_section_mul(int rt,int val, int l, int r, int rl, int rr) { //Range update *val
if (rl <= l && r <= rr) {//When current interval is a sub-interval of update range, directly update value and lazy tag
Tree[rt] = (Tree[rt] * val) % p;
mul[rt] = (mul[rt] * val) % p;
add[rt] = (add[rt] * val) % p;//Very important!!
return;
}
pushdown(rt, l, r);//Before next recursion, push down the effect
int mid = (l+r) >> 1;
if (rl <= mid)//If update range affects left half, update left subtree
Update_section_mul(rt<<1, val, l, mid, rl, rr);
if (rr > mid)
Update_section_mul(rt<<1|1, val, mid+1, r, rl, rr);//Otherwise update right subtree
pushup(rt);//Backtrack - push up
}Complete Code
#include <iostream>
#include <algorithm>
using namespace std;
//Definitions
typedef long long ll;
const int maxn = 1000005;
ll add[maxn<<2];//Lazy tag 1 - the effect on all child nodes, not including itself
ll mul[maxn<<2];//Lazy tag 2
ll Tree[maxn<<2];
ll A[maxn];
int n, T;
ll p;
inline void pushup(int rt) {//Push up to update node info - use left and right children to update current node
Tree[rt] = Tree[rt << 1]+Tree[rt << 1|1];
}
inline void f(int rt, int l, int r, int ft) {//Apply all effects of parent node ft to current node rt, update its lazy tags
//Multiply first, then add!!
Tree[rt] = (Tree[rt] * mul[ft]) % p;
Tree[rt] = (Tree[rt] + add[ft] * (r-l+1)) % p;
//mul is directly updated
mul[rt] = (mul[rt] * mul[ft]) % p;
//add lazy tag should first *parent's mul tag, then +parent's add tag!!!
add[rt] = (add[rt] * mul[ft]) % p;
add[rt] = (add[rt] + add[ft]) % p;
}
void pushdown(int rt, int l, int r) {
int mid = l+r >>1;
f(rt<<1, l, mid, rt);//Update left child's lazy tags and maintained value
f(rt<<1|1, mid+1, r, rt);//Update right child's lazy tags and maintained value
add[rt] = 0;
mul[rt] = 1;//Reset current lazy tags
}
void Build(int l, int r, int rt) {//[l,r] represents the interval, rt is the actual storage index
add[rt] = 0;
mul[rt] = 1;
if (l == r) {//Reached a leaf node
Tree[rt] = A[l];
return;
}
int mid = l+r>>1;
Build(l,mid,rt << 1);//Build the left subtree first
Build(mid+1,r,rt << 1 | 1);//Then build the right subtree
pushup(rt);//Update info using left and right children
}
void Update_section_add(int rt,int val, int l, int r, int rl, int rr) { //Range update +val
if (rl <= l && r <= rr) {//When current interval is a sub-interval of update range, directly update value and lazy tag
Tree[rt] = (Tree[rt] + val * (r-l+1)) % p;//Apply +val effect to current node and update its lazy tag
add[rt] = (add[rt] + val) % p;
return;
}
pushdown(rt, l, r);//Before next recursion, push down the effect
int mid = (l+r) >> 1;
if (rl <= mid)//If update range affects left half, update left subtree
Update_section_add(rt<<1, val, l, mid, rl, rr);
if (rr > mid)
Update_section_add(rt<<1|1, val, mid+1, r, rl, rr);//Otherwise update right subtree
pushup(rt);//Backtrack - push up
}
void Update_section_mul(int rt,int val, int l, int r, int rl, int rr) { //Range update *val
if (rl <= l && r <= rr) {//When current interval is a sub-interval of update range, directly update value and lazy tag
Tree[rt] = (Tree[rt] * val) % p;
mul[rt] = (mul[rt] * val) % p;
add[rt] = (add[rt] * val) % p;//Very important!!
return;
}
pushdown(rt, l, r);//Before next recursion, push down the effect
int mid = (l+r) >> 1;
if (rl <= mid)//If update range affects left half, update left subtree
Update_section_mul(rt<<1, val, l, mid, rl, rr);
if (rr > mid)
Update_section_mul(rt<<1|1, val, mid+1, r, rl, rr);//Otherwise update right subtree
pushup(rt);//Backtrack - push up
}
ll query(int rt, int l, int r,int x, int y) {//Query range sum of x~y from node rt in l to r
if (x <= l && r <= y) {//When l~r is a sub-interval of the query interval, return current node value directly
return Tree[rt];
}
int mid = l+r >> 1;
ll ans = 0;
pushdown(rt, l, r);
if (x <= mid) //If the left endpoint of the current interval <= mid, we must query the left half
ans = (ans + query(rt<<1,l,mid,x,y)) % p;
if (y > mid)//If the right endpoint of the current interval > mid, we must query the right half
ans = (ans + query(rt<<1|1,mid+1,r,x,y)) % p;
return ans;
}
int main(){
ios::sync_with_stdio(false);
cin >> n >> T >> p;
for(int i = 1; i <= n; i++) {
cin >> A[i];
}
Build(1,n,1);
while(T--) {
int a, l, r;
cin >> a;
if (a == 1) {
int k;
cin >> l >> r >> k;
Update_section_mul(1, k, 1, n, l, r);
} else if(a == 2) {
int k;
cin >> l >> r >> k;
Update_section_add(1, k, 1, n, l, r);
} else {
cin >> l >> r;
ll ans = query(1, 1, n, l, r);
cout << ans << endl;
}
}
return 0;
}And there you go — congratulations on getting AC!


喜欢的话,留下你的评论吧~