This article has been machine-translated from Chinese. The translation may contain inaccuracies or awkward phrasing. If in doubt, please refer to the original Chinese version.
Preface
This exam was an online dual-camera exam, for which I once again had to buy a phone stand... 92 points. I couldn't optimize my way past Problems 3 and 4, probably due to flawed approaches.
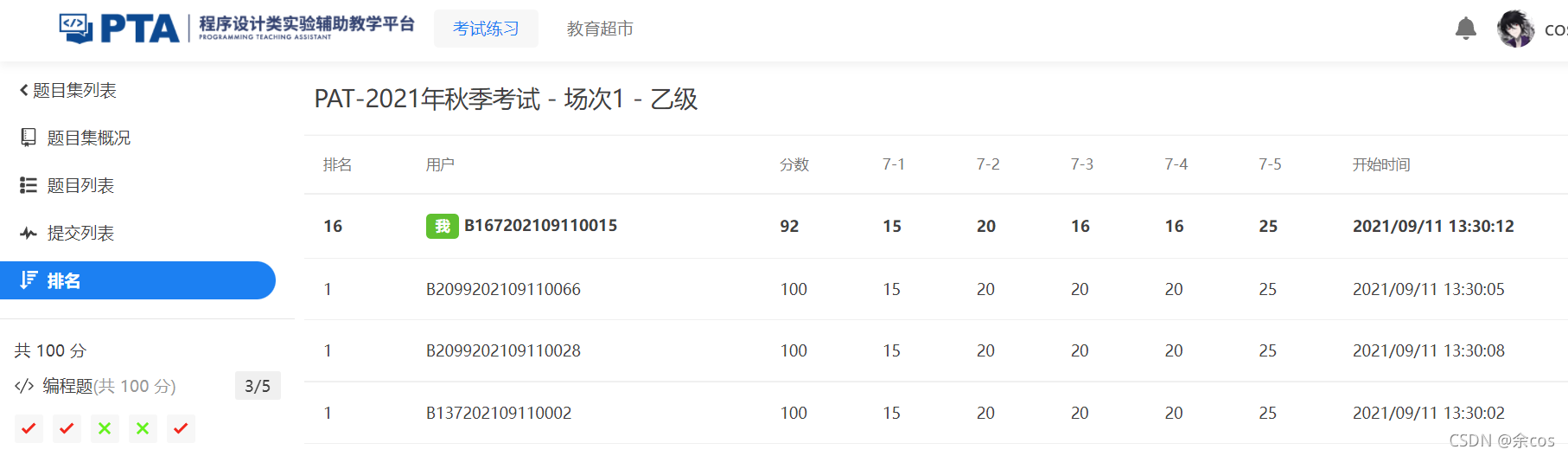
Solutions
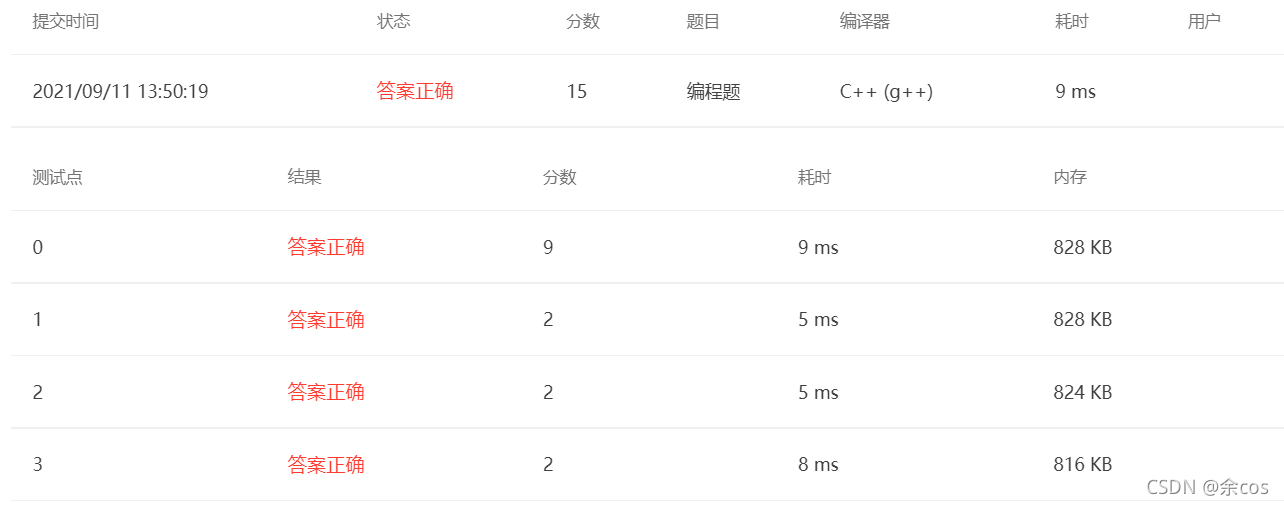
7-1 Good Numbers (15 points)
A good number is a number generated by a pair of positive integers a < b following the rule a2+ab+b2. The pair (a, b) is called the source of this good number. For example, 91 is a good number because 52+5x6+62 = 91, so the pair (5, 6) is a source of 91. However, a good number may have more than one source -- for example, (1, 9) is another source of 91. Your task is to write a program to determine whether a given number is good, and output all sources of good numbers. Input Format The first line gives a positive integer N not exceeding 100, followed by N lines, each giving a positive integer not exceeding 104. Output Format For each input number, if it is a good number, first output "Yes" on a line, then output each source on a line in the format "a b", in increasing order of a. Otherwise, output "No" followed by the smallest good number greater than the given number, separated by a space, then output each source of that good number in the same format. Sample Input
3
1
91
50Sample Output
No 7
1 2
Yes
1 9
5 6
No 52
2 6Approach
My approach was brute force. I used a bool array a to store whether a number is a good number, and a map to store all sources for each good number. Then I iterated through every pair of sources, marked the corresponding good number as true, and added it to the source array. After that, I just used a to check whether the given n is a good number. If not, search forward.
Too brute force, but hey, full marks is full marks, too lazy to optimize
Wait, the editorial is also brute force? Then never mind
Code
#include <iostream>
#include <map>
#include <vector>
#include <utility>
using namespace std;
const int maxn = 100005;
int N;
bool a[maxn];
map<int, vector<pair<int, int> > > m;
void Print(int h) {
vector<pair<int, int> > v = m[h];
for(auto i: v) {
cout << i.first << ' ' << i.second << endl;
}
}
int main() {
cin >> N;
for(int i = 1; i < 105; ++i) {
for(int j = i+1; j < 106; ++j) {
int x = i*i+i*j+j*j;
// cout << x << endl;
m[x].push_back(make_pair(i, j));
a[x] = true;
}
}
int k;
while(N--) {
cin >> k;
if(!a[k]) {
while(!a[k]) ++k;
cout << "No " << k << endl;
} else cout << "Yes" << endl;
Print(k);
}
return 0;
}
7-2 Birds of a Feather (20 points)
We group all numbers whose digit products are the same into one class. For example, 1362 and 2332 are in the same class because 1x3x6x2=2x3x3x2. Given N positive integers, how many different classes can they be grouped into? Input Format The first line gives a positive integer N (<=105), and the second line gives N positive integers not exceeding 107, separated by spaces. Output Format In one line, output the number of classes the N given integers can be grouped into, and the smallest product among the largest class. Numbers are separated by a space. Sample Input
10
1234 98 329 9552 47621 8862 5539 2333 5365 463Sample Output
7 54Approach
Brute force
A tran function returns the product of all digits of number x (returns 0 directly if there's a 0).
Then during input, we can start recording. A map represents the size of each class, where m[i] represents how many numbers have digit product i.
Code
#include <iostream>
#include <sstream>
#include <map>
#include <vector>
#include <set>
#include <algorithm>
using namespace std;
typedef long long ll;
const ll maxn = 100005;
ll N, x;
map<ll, ll> m;// 每个类的规模
set<ll> s;// 类的个数
ll tran(ll x) {
string str;
stringstream ss;
ss << x;
ss >> str;
if(str.find('0') != string::npos) return 0;
int len = str.length();
ll ans = 1;
for(int i = 0; i < len; ++i) {
ll c = str[i]-'0';
ans *= c;
}
return ans;
}
int main() {
cin >> N;
for(int i = 0; i < N; ++i) {
cin >> x;
ll t = tran(x);
++m[t];
s.insert(t);
}
ll maxi = -1;
ll ans = maxn;
for(auto i: s) {
if(m[i] >= maxi)
maxi = m[i];
}
for(auto i: s) {
if(m[i] == maxi && i < ans) ans = i;
}
cout << s.size() << ' ' << ans << endl;;
return 0;
}7-3 Custom Judging Program (20 points)
Given the minimum number of operations to transform one string into another (with each operation being insert, delete, or modify one character), this is a famous problem solvable by dynamic programming. The difficulty in judging is that while the minimum cost is unique, the transformation method is not. For example, transforming PAT to PTA requires at least 2 steps: you can keep the 1st letter and modify the last 2, or keep the 1st and 2nd letters, insert T before A, and delete the trailing T. Since the default judging program can only compare output files, it cannot handle problems with non-unique correct answers, requiring a custom judging program. Your task is to write this custom judging program: read two strings and the user's output, and determine whether their output is correct. Input Format The first two lines give two non-empty strings of at most 1000 characters each, ending with newlines. Line 1 is the initial string, line 2 is the target string.
The next line gives a positive integer N (<=100), the number of submissions to judge.
Then come N submissions, each taking 2 lines: line 1 gives an integer K (within 32-bit int range), the user's reported number of operations; line 2 sequentially describes the operation for each character of the initial string:
- If the character is unchanged, output 0 at the corresponding position
- If the character is deleted, output 1 at the corresponding position
- If the character is modified, output 2 at the corresponding position
- If a character is inserted before or after this character, output 3 at the insertion position
Note that we require no spaces at the beginning, end, or between numbers in the user's submission, so extra spaces should be judged as errors.
The problem guarantees this operation sequence is non-empty. Output Format For each correct submission, output AC on a line; otherwise output WA.
Note: You are NOT required to use dynamic programming to find the optimal solution. The "correct submission" is NOT based on the optimal solution from DP! For a user's output K, if the operation sequence indeed performs K operations and can complete the string transformation, it is called a "feasible solution." A "correct submission" is the optimal solution among all submitted feasible solutions. Sample Input
This is a test.
Tom is a cat.
6
8
02330001100022100
8
11113330000001113300
6
022100000012200
5
033310000000200
6
0 2 2 1 000000 1 2 2 00
6
012200000022100Sample Output
WA
WA
AC
WA
WA
ACApproach
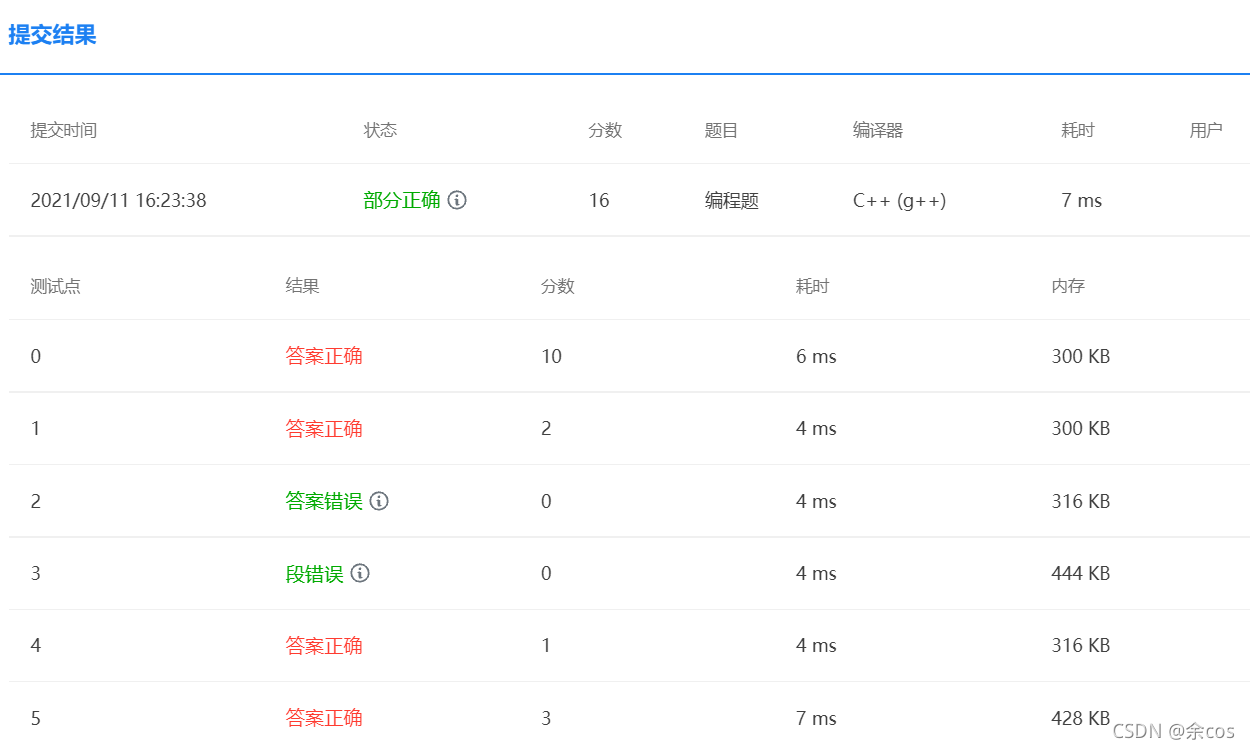
In the last 10 minutes I went from 12 to 16 points, but something's still off. Probably an issue with the termination condition.
The problem asks: given two strings and a series of operations, for each operation determine whether it is valid, can transform the initial string into the target string, and is the optimal solution (the best among all submitted feasible solutions).
Read s1, s2, then read operations: operation count K and operation string t. First check if the operation is valid (no spaces, and the count of 0/1/2 equals K), then use the judge function to check whether each step is feasible, manually simulating no-change, delete, modify, and insert.
Code
#include <iostream>
#include <string>
#include <vector>
using namespace std;
typedef long long ll;
const ll inf = INT32_MAX;
string s1, s2, t;
int N, minK;
ll K;
vector<string> v;
vector<bool> b;
vector<int> ck;
bool judge(string s) {
for(int i = 0; i < s.size(); ++i) if(s[i] == ' ') return false;
int cnt = 0;//操作数
string temp;
int k1 = 0;
int k2 = 0; //s1下标
int len = s.length();
int len1 = s1.length();
int len2 = s2.length();
for(int i = 0; i < len; ++i) {
if(s[i] == '0') { // 不变
temp += s2[k2++];
++k1;
} else if(s[i] == '1') { // 删除
++cnt, ++k1;
} else if(s[i] == '2'){ // 被改变
temp += s2[k2++];
++cnt, ++k1;
} else { // 插入
++cnt;
if(s1[k1] != s2[k2]) { //在前面插入
temp += s2[k2++];
} else { //相同的话在后面插入,或者如果后面也相同的话前插
temp += s2[k2++];
temp += s2[k2++];
++k1;
}
}
}
// cout << temp << endl;
if(temp == s2 && cnt == K) return true;
else return false;
}
int main() {
getline(cin, s1);
getline(cin, s2);
cin >> N;
minK = inf;
for(int i = 0; i < N; ++i) {
cin >> K;
ck.push_back(K);
cin.ignore();
getline(cin, t);
v.push_back(t);
// cout << K << t << endl;
b.push_back(judge(t));
if(b[i] && K < minK) minK = K;
}
// cout << minK << endl;
for(int i = 0; i < v.size(); ++i) {
if(b[i] && ck[i] == minK) cout << "AC" << endl;
else cout << "WA" << endl;
}
return 0;
}7-4 Arrays and Linked Lists (20 points)
Let's design a data structure A that combines arrays and linked lists for integer storage:
This structure first initializes an integer array A0 of length L0 and returns it for user use. When the user accesses element A[i], if 0<=i<L0, then A[i] corresponds to A0[i], and the system returns h0 + i x sizeof(int) as the address to access, where h0 is the starting position of array A0 and sizeof(int) is the element size (int, 4 bytes).
When the user accesses out of bounds (i>=L0), the system allocates another array A1 of length L1. Then A[i] corresponds to A1[j] (the mapping between i and j is left for you to derive). If 0<=j<L1, it returns h1+j x sizeof(int), where h1 is the starting position of A1.
When A1[j] continues to be out of bounds, the system follows the same rules to allocate another array A2 of length L2, and so on.
Your task is to implement this system and return the corresponding element address for any user access.
Input Format
The first line gives two positive integers N (<=104) and K (<=103), representing the maximum number of arrays that can be allocated and the number of user accesses.
The next N lines each give two positive integers: an array's starting address (<=107) and length (<=100), separated by spaces. The problem guarantees these arrays' spaces don't overlap.
The last line gives K user access indices, integers in the range [0, 220].
Output Format
For each user access, output the corresponding address on a line. If the access exceeds the storage range of all N arrays, the access is illegal -- output Illegal Access and take no action for this access.
The last line should output how many arrays were created in total during the process. Sample Input
6 7
2048 5
128 6
4016 10
1024 7
3072 12
9332 10
2 12 25 50 28 8 39Sample Output
2056
4020
1040
Illegal Access
3072
140
3116
5Approach
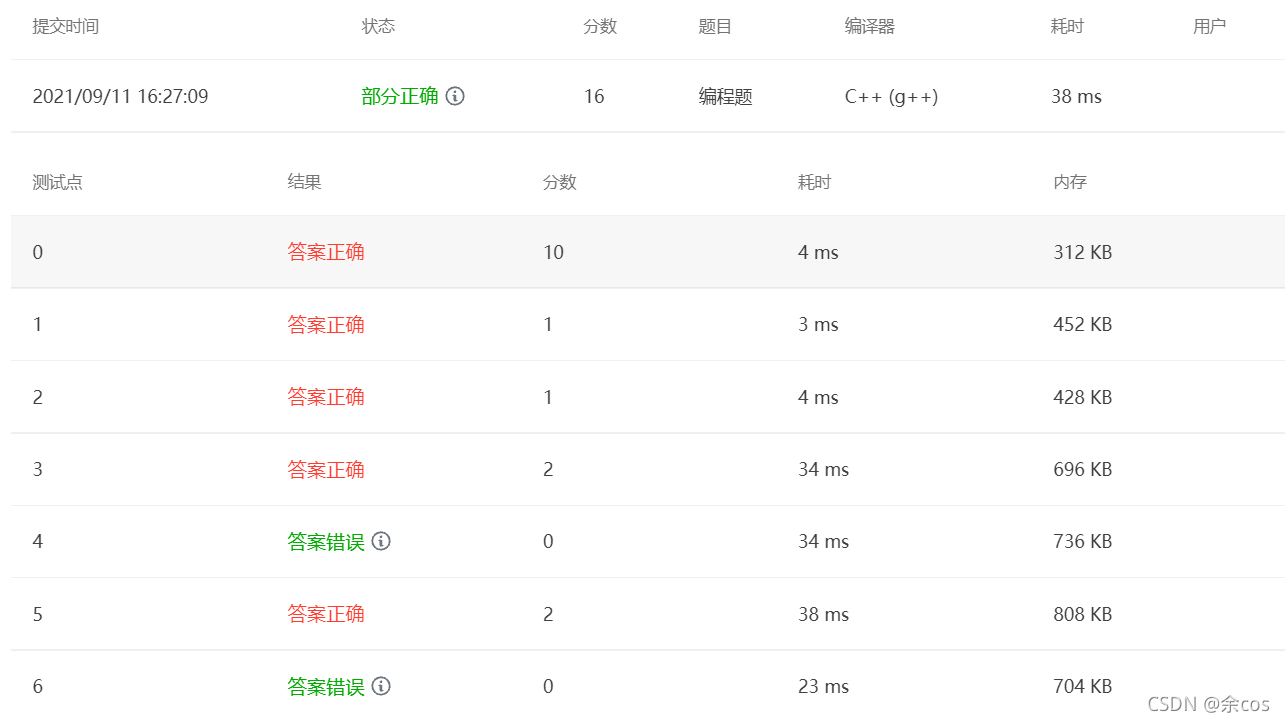
Also 16 points, let me see where it went wrong
The linked list is given in array form, providing each segment's starting address and the number of elements it can hold. Int data occupies 4 bytes. We need to determine whether an element can fit in the current array and what its address would be. First read all data and calculate the capacity, then sequentially read K user access indices and check whether they exceed the current array's bounds. If so, allocate more arrays.
Code
#include <iostream>
#include <string>
#include <vector>
using namespace std;
typedef long long ll;
int N, K;
ll x, nowx, cnt;
struct Arr {
ll adr;
int len;
} a;
vector<Arr> v;
int main() {
cin >> N >> K;
for(int i = 0; i < N; ++i) {
cin >> a.adr >> a.len;
v.push_back(a);
}
int realans = 1;
for(int i = 0; i < K; ++i) {
int ans = 1;
bool flag = false;
cin >> x;
cnt = 0;
for(int j = 0; j < v.size(); ++j) {
if(flag) break;
if(x >= cnt+v[j].len) { //越这个数组界了 加开数组
cnt += v[j].len;
++ans;
continue;
} else {
// cout << cnt << ' ';
flag = true;
cout << v[j].adr+(x-cnt)*4 << endl;
}
}
if(!flag) cout << "Illegal Access" << endl;
else realans = ans;
}
cout << realans << endl;
return 0;
}
//2048+87-5 Getting Hats (25 points)
Problem solvers think wearing hats makes them look cool, so they wear hats everywhere. One day they went to a restaurant, and the waiter collected and stacked their hats. When everyone was about to leave, they found the hats were stacked like the picture above. Your task is to line them up so that everyone can get their hat in order. Each hat has a different size, and hat size is related to the owner's weight -- heavier people wear larger hats. Input Format The first line gives a positive integer N (<=104), the number of people. The next line gives N distinct hat sizes as positive integers not exceeding 105, listed from bottom to top of the hat pile. The last line gives N distinct weights corresponding to people numbered 1 to N. Weights are positive integers not exceeding 106. Numbers on a line are separated by spaces. Output Format Output the owners' numbers in the order of hat retrieval on one line. Numbers are separated by 1 space, with no extra spaces at the beginning or end. Sample Input
10
12 19 13 11 15 18 17 14 16 20
67 90 180 98 87 105 76 88 150 124Sample Output
3 4 8 6 10 2 1 5 9 7Approach
The easiest problem is worth 25 points?!
Given N hat sizes (from bottom to top) and N people's weights (numbered 1-N), heavier weight corresponds to larger hat. Output the queuing order so everyone can get their hat.
Just need two arrays v1, v2 for hat sizes and weights, and two maps m2, m3. m2[i] represents the number of the person with weight i, and m3[i] represents the index after sorting hat size i.
Code
#include <iostream>
#include <algorithm>
#include <vector>
#include <map>
using namespace std;
const int maxn = 10005;
int N, x;
int a[maxn];
int b[maxn];
vector<int> v1;
vector<int> v2;
map<int, int> m2;
map<int, int> m3;
int main() {
cin >> N;
for(int i = 0; i < N; ++i) {
cin >> a[i];
v1.push_back(a[i]);
}
for(int i = 0; i < N; ++i) {
cin >> b[i];
v2.push_back(b[i]);
m2[b[i]] = i;
}
sort(v1.begin(), v1.end());
for(int i = 0; i < v1.size(); ++i) {
m3[v1[i]] = i; //20对应v1排好序的下表
}
sort(v2.begin(), v2.end());
cout << m2[v2[m3[a[N-1]]]]+1;
for(int i = N-2; i >= 0; --i) {
cout << ' ' << m2[v2[m3[a[i]]]]+1;
}
cout << endl;
return 0;
}
喜欢的话,留下你的评论吧~