This article has been machine-translated from Chinese. The translation may contain inaccuracies or awkward phrasing. If in doubt, please refer to the original Chinese version.

Record of the 2020 Lanqiao Cup mock provincial contest problems and code. Corrections are welcome! Since there were no scores after the contest, I don’t know which problems were correct or incorrect. I can only rely on my intuition during the contest, so there may be omissions.

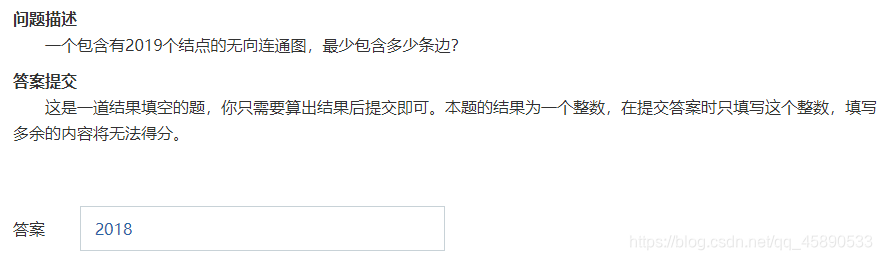
1. Fill-in-the-Blank Problem

Obviously the answer is 2018

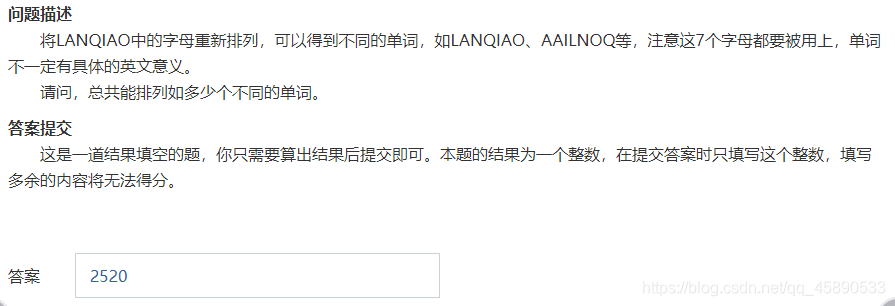
2. Fill-in-the-Blank Problem

Since two letters are repeated, the answer is 7! / 2 = 2520

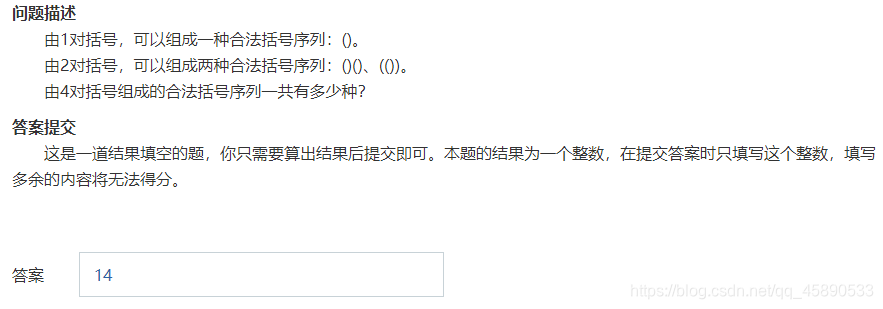
3. Fill-in-the-Blank Problem

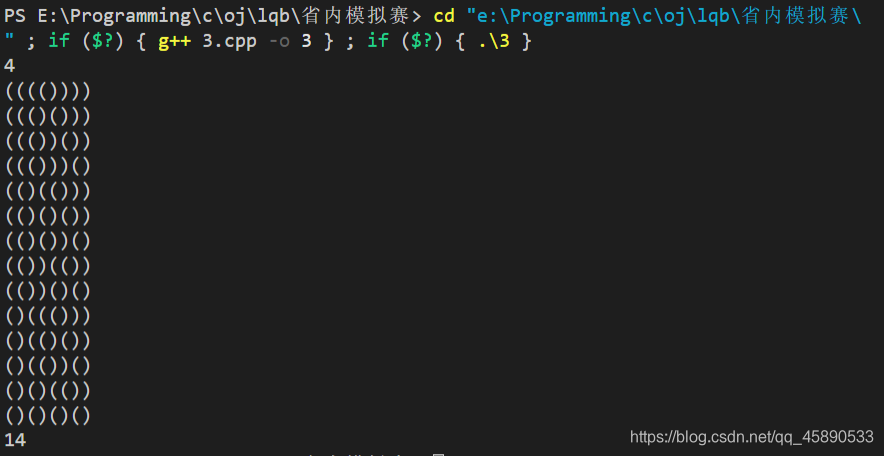
4 pairs of parentheses, enumeration gives 14 cases in total. Alternatively, you can use recursion.

#include <iostream>
#include <vector>
using namespace std;
typedef long long ll;
ll n,ans,total;//total表示要排的几对括号
vector<char> v;
void Permu(int sum,int l,int r) {//剩余待排列括号数 已经排好的括号数
    if(l < r) return;   //先排左括号再排右括号，且右括号一定是与左括号匹配的
    //所以左括号只能>=右括号
    if(sum == 0) {
        ans++;
        vector<char>::iterator it;
        for(it = v.begin(); it != v.end(); it++) {
            cout << *it;
        }
        cout << endl;
    }
    if(l < total) {
        v.push_back('(');
        Permu(sum-1,l+1,r);
        v.pop_back();
    }
    if(r < total) {
        v.push_back(')');
        Permu(sum-1,l,r+1);
        v.pop_back();
    }
}
int main() {
    cin >> total;
    Permu(total*2,0,0);
    cout << ans << endl;
    return 0;
}

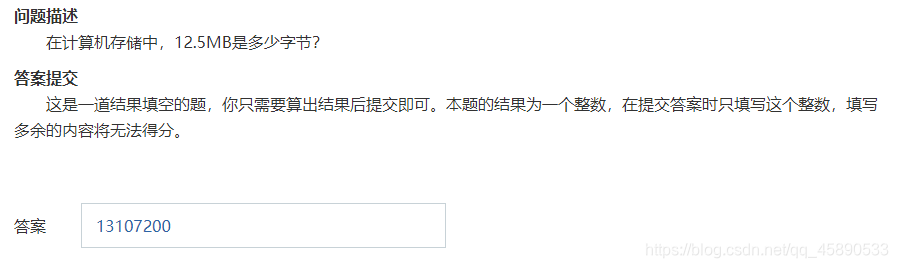
4. Fill-in-the-Blank Problem

Free points, 12.5 * 1024 * 1024 = 13107200

5. Programming Problem

String processing, just take modulo 26 to prevent overflow.

#include <iostream>
#include <string>
#define div 1000000007
typedef long long ll;
const int maxn = 100;
using namespace std;
string s;
int main() {
    cin >> s;
    int len = s.length();
    for (int i = 0; i < len; i++) {
        s[i] = 'a' + (s[i]-'a'+3)%26;
    }
    cout << s << endl;
    return 0;
}

6. Programming Problem

O(n) complexity should be able to pass all test cases… probably.

#include <iostream>
#include <string>
#define div 1000000007
typedef long long ll;
const int maxn = 1000000;
using namespace std;
ll n, a, b, c, ans;
int main() {
    cin >> n;
    cin >> a >> b >> c;
    for (int i = 1; i <= n; i++) {
        if(i % a != 0 && i % b != 0 && i % c != 0) {
            ans++;
        }
    }
    cout << ans << endl;
    return 0;
}

7. Programming Problem

Quite similar to a problem from the school mock contest. I used memoized recursion. The sample passes, and the speed should handle 80%. Please point out any logical flaws.

Problem Description If the odd-indexed terms of a sequence are all greater than the previous term, and even-indexed terms are all less than the previous term, it is called a swing sequence. That is, a[2i]<a[2i-1], a[2i+1]>a[2i]. Xiao Ming wants to know how many swing sequences of length m exist, where each number is a positive integer between 1 and n. Input Format Input contains two integers m and n on one line. Output Format Output an integer representing the answer. The answer may be very large, so please output the remainder when divided by 10000. Sample Input 3 4 Sample Output 14 Sample Explanation The following are the valid swing sequences: 2 1 2 2 1 3 2 1 4 3 1 2 3 1 3 3 1 4 3 2 3 3 2 4 4 1 2 4 1 3 4 1 4 4 2 3 4 2 4 4 3 4 Test Case Scale and Constraints For 20% of test cases, 1 <= n, m <= 5; For 50% of test cases, 1 <= n, m <= 10; For 80% of test cases, 1 <= n, m <= 100; For all test cases, 1 <= n, m <= 1000.

#include <iostream>
#include <cstring>
#define div 10000
typedef long long ll;
const int maxn = 1000000;
using namespace std;
int n, m;
ll ans;
int rem[101][101][101];
ll dfs(int m,int l, int r){
    //长度为 m，每个数都是 l 到 r 之间的正整数的摆动序列一共有多少个
    if(rem[m][l][r] != -1) return rem[m][l][r];
    if(l > r) {
        rem[m][l][r] = 0;
        return rem[m][l][r];
    } else if(l == r) {
        rem[m][l][r] = 1;
        return rem[m][l][r];
    } else if(m == 1) {
        rem[m][l][r] = r-l+1;
        return rem[m][l][r];
    }

    if(m % 2 == 0) {//偶数项都比前一项小 则前一项只能在i~r
        for(int i = l; i <= r; i++) {
            ans = (ans + dfs(m-1,i+1,r)) % div;
        }
    } else {//奇数项都比前一项大 则前一项只能在l~i
        for(int i = l; i <= r; i++) {
            ans = (ans + dfs(m-1,l,i-1)) % div;
        }
    }
    rem[m][l][r] = ans%div;
    return rem[m][l][r];
}
int main() {
    memset(rem,-1,sizeof(rem));
    cin >> m >> n;
    cout << dfs(m,1,n) << endl;
    return 0;
}

8. Programming Problem

Spiral matrix. Once you know the maximum number of steps, it’s straightforward. The order is: right, down, left, up.

Problem Description For an n-row m-column table, we can fill the table with positive integers in a spiral manner. The filled table is called a spiral matrix. For example, a 4-row 5-column spiral matrix is as follows: 1 2 3 4 5 14 15 16 17 6 13 20 19 18 7 12 11 10 9 8 Input Format The first line of input contains two integers n and m, representing the number of rows and columns of the spiral matrix. The second line contains two integers r and c, representing the requested row and column numbers. Output Format Output an integer representing the value at row r, column c in the spiral matrix. Sample Input 4 5 2 2 Sample Output 15 Test Case Scale and Constraints For 30% of test cases, 2 <= n, m <= 20. For 70% of test cases, 2 <= n, m <= 100. For all test cases, 2 <= n, m <= 1000, 1 <= r <= n, 1 <= c <= m.

#include <iostream>
#include <cstring>
#define div 10000
typedef long long ll;
const int maxn = 1000000;
using namespace std;
int n, m;
int k = 1;
int a[105][105];
int main() {
    cin >> n >> m;
    int all = n*m;
    int r=1, c=1;//行 列
    a[r][c] = k;
    while(k < all) {//进行上下左右的判断
        while(c+1 <= m && !a[r][c+1]) {//当右边没走过且未出界时 向右走
            a[r][++c] = ++k;
        }
        while(r+1 <= n && !a[r+1][c]) {//当下边没走过且未出界时 向下走
            a[++r][c] = ++k;
        }
        while(c-1 >= 1 && !a[r][c-1]) {//当左边没走过且未出界时 向左走
            a[r][--c] = ++k;
        }
        while(r-1 >= 1 && !a[r-1][c]) {//当上边没走过且未出界时 向上走
            a[--r][c] = ++k;
        }
    }
    cin >> r >> c;
    cout << a[r][c] << endl;
    return 0;
}

9. Programming Problem

Not yet solved.

Problem Description Xiao Ming and his friends went to the countryside to plant trees. They brought some saplings carefully developed in their own lab. Xiao Ming and his friends have n people in total. After careful selection, each person picked a suitable planting position on a clearing, totaling n positions. They plan to plant all the saplings they brought. However, they encountered a difficulty: some saplings are quite large, and some positions are too close together, causing two trees to collide if planted. They model each tree as a circle, centered at the chosen position. If two trees’ corresponding circles intersect, these two trees are not suitable to be planted simultaneously (tangency is fine), which is called a conflict between two trees. Xiao Ming and his friends decided to discuss and plant only a subset of the trees, ensuring no conflicts. They also want the total area covered by these trees (sum of circle areas) to be maximized. Input Format The first line contains an integer n, representing the number of people, i.e., the number of planting positions. The next n lines each contain three integers x, y, r, representing a tree’s horizontal coordinate, vertical coordinate, and radius on the clearing. Output Format Output one line containing an integer representing the maximum sum of plantable areas without conflicts. Since each tree’s area is an integer multiple of pi, please output the answer divided by pi (which should be an integer). Sample Input 6 1 1 2 1 4 2 1 7 2 4 1 2 4 4 2 4 7 2 Sample Output 12 Test Case Scale and Constraints For 30% of test cases, 1 <= n <= 10; For 60% of test cases, 1 <= n <= 20; For all test cases, 1 <= n <= 30, 0 <= x, y <= 1000, 1 <= r <= 1000.

10. Programming Problem

This is essentially a minimum spanning tree problem. I learned Prim’s algorithm on the spot and submitted in the last few minutes. The sample passes, but I haven’t tested for bugs yet.

Problem Description In 2015, every household in China had electricity. As a power construction worker, Xiao Ming is now helping countries along the Belt and Road get connected. This time, Xiao Ming needs to connect n villages with electricity. Village 1 happens to have a power station that generates enough electricity for all villages. Currently, there are no power lines connecting these n villages. Xiao Ming’s main task is to set up power lines to connect all villages, so that all villages are directly or indirectly connected to the power station. Xiao Ming measured all village positions (coordinates) and heights. To connect two villages, Xiao Ming needs to spend the coordinate distance between two villages plus the square of the height difference. Formally, connecting a village at coordinates (x1, y_1) with height h_1 to a village at coordinates (x_2, y_2) with height h_2 costs sqrt((x_1-x_2)(x1-x_2)+(y_1-y_2)(y_1-y_2))+(h_1-h_2)*(h_1-h_2). In the formula above, sqrt means taking the square root of the content inside the parentheses. Note the position of parentheses - the calculation for height is different from that for coordinates. Given limited budget, please help Xiao Ming calculate the minimum cost to connect all n villages with electricity. Input Format The first line contains an integer n, representing the number of villages. The next n lines each contain three integers x, y, h, representing a village’s horizontal coordinate, vertical coordinate, and height. The first village can have a power station. Output Format Output one line containing a real number rounded to 2 decimal places, representing the answer. Sample Input 4 1 1 3 9 9 7 8 8 6 4 5 4 Sample Output 17.41 Test Case Scale and Constraints For 30% of test cases, 1 <= n <= 10; For 60% of test cases, 1 <= n <= 100; For all test cases, 1 <= n <= 1000, 0 <= x, y, h <= 10000.

#include <iostream>
#include <cstring>
#include <cmath>
#define div 10000
typedef long long ll;
const int maxn = 1000;
const int INF = 0x3f3f3f;
using namespace std;
int n, m;
struct Village{
    int x,y,h;
} v[maxn];
double edge[maxn][maxn];
int fa[maxn];//fa[i]表示已加入的V中里该点最近的点编号
int vis[maxn];//该点是否已访问过
double dist[maxn];
double ans;
//sqrt((x_1-x_2)*(x_1-x_2)+(y_1-y_2)*(y_1-y_2))+(h_1-h_2)*(h_1-h_2)。
void init() {
    for(int i = 2; i <= n; i++) {
        dist[i] = edge[1][i];
    }
    fa[1] = -1;
    vis[1] = 1;////收录初始点1
}
double Prim() {
    init();
    for(int i = 2; i <= n; i++) {
        int min = INF;
        int v = -1;
        for(int j = 2; j <= n; j++) {
            if(!vis[j] && dist[j] < min) {
                min = dist[j];
                v = j;
            }
        }
        if(v != -1) {//找到了最小的~收入V
            vis[v] = 1;
            ans += dist[v];
            for(int j = 2;j <= n; j++) {//更新距离dist
                if(!vis[j] && edge[v][j] < dist[j]) {
                    dist[j] = edge[v][j];
                    fa[j] = v;
                }
            }
        }
    }
    return ans;
}
int main() {
    cin >> n;
    for(int i = 1; i <= n; i++) {
        cin >> v[i].x >> v[i].y >> v[i].h;
    }
    for(int i = 1; i <= n; i++) {
        for(int j = 1; j <= n; j++) {
            if(i == j) continue;
            double d = sqrt((v[i].x-v[j].x)*(v[i].x-v[j].x)+(v[i].y-v[j].y)*(v[i].y-v[j].y))
                 +(v[i].h-v[j].h)*(v[i].h-v[j].h);
            edge[i][j] = edge[j][i] = d;
        }
    }
    double ans = Prim();
    printf("%.2f",ans);
    return 0;
}

Summary

In this mock contest, my actual skill level should have been around 8 problems. Since I learned minimum spanning tree on the spot for the last problem, I wasn’t very proficient. I plan to practice more problems of this type and study graph theory more seriously.